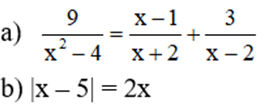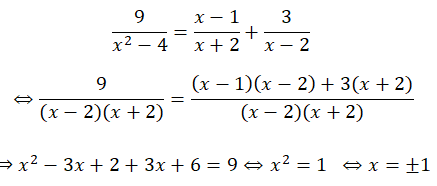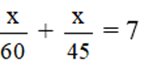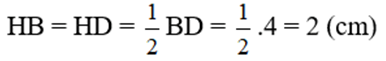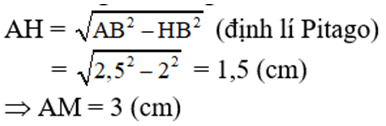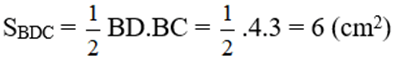Câu 4 nhoa. Ai trả lời đc thì tick.✔ .
Giúp cái 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 3 2021
"Lượm" là một trong những bài thơ hay của nhà văn Tố Hữu được đông đảo thế hệ học sinh yêu thích(1).Bài thơ ra đời năm 1949 trong thời kỳ kháng chiến chống thực dân Pháp(2).Bài thơ kể về cuộc đời cách mạng của Lượm(3).Chú bé Lượm hiện lên thật ngây thơ,tinh nghịch,hăng hái(4).Lượm là chú bé liên lạc trên chiến trường đầy nguy hiểm, cạm bẫy luôn rình rập cậu(5).Nhưng vì lòng yêu nước và sự dũng cảm của mình Lượm đã xuất sắc hoàn thành những nhiệm vụ được giao(6).Trong một lần đi giao thư "Thượng khẩn" Lượm đã hy sinh, chú bé ngã xuống ngay trên cánh đồng quê hương và cánh đồng như ôm Lượm vào lòng(7).Tuy Lượm đã hy sinh nhưng hình ảnh của chú còn mãi với quê hương, đất nước và trong lòng mọi người(8).Bằng thể thơ bốn chữ, kết hợp miêu tả và biểu hiện cảm xúc bài thơ đã khắc họa thành công hình ảnh chú bé Lượm(9).Tấm gương dũng cảm và lòng yêu nước của Lượm đáng để mọi người noi theo(10).
11 tháng 4 2020
Mỗi bạn được số cái kẹo dẻo là và số kẹo dư là
2463:9=273 (cái kẹo) và dư 6 (cái kẹo)
Đáp số: 273 cái kẹo và dư 6 cái kẹo
T
29 tháng 5 2021
20% x X + 0,4 x X = 12
=> \(\frac{\text{1}}{\text{5}}\)x X + \(\frac{\text{2}}{\text{5}}\)x X = 12
=> X x \(\left(\frac{\text{1}}{\text{5}}+\frac{\text{2}}{\text{5}}\right)\)=12
=> X x \(\frac{\text{3}}{\text{5}}\)=12
=> x = 20
Vậy x = 20
29 tháng 5 2021
\(\frac{20}{100}\times x+\frac{4}{10}\times x=12\)
\(\left(\frac{1}{5}+\frac{2}{5}\right)\times x=12\)
\(\frac{3}{5}\times x=12\)
\(x=12:\frac{3}{5}\)
\(x=\frac{4}{5}\)
L
6
1G
5
4 tháng 10 2016
4 ^300 và 3 ^400
ta có 4 ^300= 4 ^3.100= 4^3 ( 100) = 64 ^ 100
3 ^ 400= 3 ^4.100= ( 3^4) ^100 = 81 ^100
Vì 64 < 81 nên 4 ^ 300 < 3 ^ 400
15 tháng 5 2019
Kham khảo đề tự luận này nè bọn mình thi chúng đấy
Câu 1 (2,0 điểm) Thực hiện phép tính:
a) 2xy.3x2y3
b) x.(x2 - 2x + 5)
c) (3x2 - 6x) : 3x
d) (x2 – 2x + 1) : (x – 1)
Câu 2 (2,0 điểm). Phân tích các đa thức sau thành nhân tử:
a) 5x2y - 10xy2
b) 3(x + 3) – x2 + 9
c) x2 – y2 + xz - yz
Câu 3 (2,0 điểm). Cho biểu thức: 
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?
b) Rút gọn biểu thức A.
c) Tìm giá trị của biểu thức A tại x = 1.
Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA.
Câu 5 (0,5 điểm). Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
15 tháng 5 2019
Tham khảo nek :
Bài 1: (3 điểm) Giải phương trình và bất phương trình:
C) x – 2)2 + 2(x – 1) ≤ x2 + 4
Bài 2: (2 điểm) Một ô tô đi từ A đến B với vận tốc 60km/h và đi từ B về A với vận tốc 45km/h. Thời gian cả đi và về hết 7 giờ. Tính quãng đường AB.
Bài 3: (1 điểm)Chứng minh rằng nếu a + b = 1 thì a2 + b2 ≥ 1/2
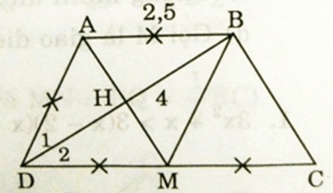
Bài 4: (4 điểm) Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
Đáp án và Hướng dẫn giải
Bài 1
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Bài 2
Gọi x (km) là quãng đường AB (x > 0)
Thời gian đi từ A đến B là: x/60 (giờ)
Thời gian đi từ B về A là: x/45 (giờ)
Theo đề ra, ta có phương trình:
⇔ 3x + 4x = 7.180 ⇔ 7x = 7.180 ⇔ x = 180 (nhận)
Trả lời: Quãng đường AB dài 180km.
Bài 3
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
Bài 4
a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
Xét tam giác vuông AHB, ta có :
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
19 tháng 4 2020
1.tay phải
2.bàn chải đánh răng
3.
4.sút vào trái bóng
5.trái bắp
19 tháng 4 2020
1.Tay phải 2.bàn chải đánh răng 3.Đỉnh núi Everest 4.Sút vào trái bóng 5 . Bắp ngô