Chứng minh rằng:x+x2-3<0 với mọi số thực x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C8
2
12 tháng 11 2021
\(x^2-2x+2021=\left(x^2-2x+1\right)+2020=\left(x-1\right)^2+2020\ge2020>0,\forall x\)
12 tháng 11 2021
x²-2x+2021=2020,875+(x-\(\dfrac{\text{1}}{\text{2}}\))2
\((x-1/2)^2\)≥0
vậy \((x-1/2)^2\)+2020,875>0
HT
2
M
3 tháng 11 2015
\(x-x^2-3=-x^2+x-\frac{1}{4}-\frac{11}{4}=-\left(x-\frac{1}{2}\right)^2-\frac{11}{4}\)
Vì \(-\left(x-\frac{1}{2}\right)\le0\Rightarrow-\left(x-\frac{1}{2}\right)-\frac{11}{4}\le\frac{-11}{4}\)
Mà \(\frac{-11}{4}<0\Rightarrow-\left(x-\frac{1}{2}\right)-\frac{11}{4}<0\)
Vậy \(x-x^2-3<0\)
PT
1
CM
16 tháng 8 2017
Ta có:
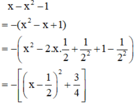
Ta có: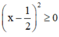 
với mọi số thực x
⇒ 
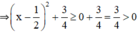với mọi số thực x
⇒ 
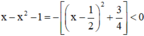với mọi số thực (ĐPCM)
F
3
H9
HT.Phong (9A5)
CTVHS
10 tháng 8 2023
Ta có:
\(x^2-x+1\)
\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\) và \(\dfrac{3}{4}>0\)
Nên: \(x^2-x+1>0\)
G
10 tháng 8 2023
\(x^2-x+1\)
\(=x^2-\dfrac{1}{2}.x-\dfrac{1}{2}.x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=x\left(x-\dfrac{1}{2}\right)-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi x ( đpcm )
TV
1
TN
0
NN
2
8 tháng 8 2021
Ta có: \(-x^2+3x-4\)
\(=-\left(x^2-3x+4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\right)\)
\(=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{7}{4}< 0\forall x\)
8 tháng 8 2021
$-x^2+3x-4\\=-x^2+2.x.\dfrac{3}{2}-\dfrac{9}{4}-\dfrac{7}{4}\\=-(x-\dfrac{3}{2})^2-\dfrac{7}{4}<0$
=> ĐPCM
NB
0
KC
1