Cho tam giác ABC có đường trung tuyến AM= 1/2 BC. Chứng mik rằng tam giác ABC vuông.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
6
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
CM
25 tháng 10 2017
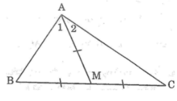
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
Vậy ΔABC vuông tại A.
13 tháng 5 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: BM=CM=BC/2=8(cm)
nên AM=6(cm)
DD
Đoàn Đức Hà
Giáo viên
1 tháng 8 2021
\(AM=\frac{1}{2}BC=BM=CM\)
suy ra \(\Delta AMB,\Delta AMC\)đều cân tại \(M\).
suy ra \(\widehat{MAB}=\widehat{MBA},\widehat{MCA}=\widehat{MAC}\)
\(\Rightarrow\widehat{ABC}=\widehat{MAB}+\widehat{MAC}=\widehat{MBA}+\widehat{MCA}=\widehat{CBA}+\widehat{BCA}\)
\(\Rightarrow\widehat{ABC}=\frac{180^o}{2}=90^o\)
Ta có đpcm.
AH
Akai Haruma
Giáo viên
27 tháng 10 2021
Lời giải:
Trên tia đối tia $MA$ lấy $D$ sao cho $MD=MA$
Dễ cm $\triangle BMA=\triangle CMD$ (c.g.c)
$\Rightarrow \widehat{MBA}=\widehat{MCD}$
Mà 2 góc này so le trong nên $BA\parallel CD$
$\Rightarrow CD\perp AC$ hay $\widehat{DCA}=90^0$
Cùng từ 2 tam giác bằng nhau trên suy ra $BA=CD$
Xét tam giác $BAC$ và $DCA$ có:
$BA=DC$
$\widehat{BAC}+\widehat{DCA}=90^0$
$AC$ chung
$\Rightarrow BC=DA$
Mà $DA=2AM$ nên $BC=2AM$
