Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
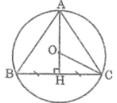
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
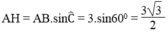
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
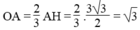
Vậy chọn đáp án C.
a) \(BM.CN=\dfrac{a^2}{4}=\dfrac{a}{2}.\dfrac{a}{2}=\dfrac{BC}{2}.\dfrac{BC}{2}=BH.HC\)
\(\Rightarrow\dfrac{BM}{BH}=\dfrac{HC}{CN}\)\(\Rightarrow\)△BMH∼△CHN (c-g-c)
\(\Rightarrow\widehat{BMH}=\widehat{CHN}\)
\(\widehat{MHN}=180^0-\widehat{BHM}-\widehat{CHN}=180^0-\widehat{BHM}-\widehat{BMH}=\widehat{MBH}=60^0\)
b) △BMH∼△CHN \(\Rightarrow\dfrac{BM}{CH}=\dfrac{MH}{HN}\Rightarrow\dfrac{BM}{BH}=\dfrac{MH}{HN}\)
\(\Rightarrow\)△HMN∼△BMH (c-g-c)
c) \(\Rightarrow\widehat{HMN}=\widehat{BMH}\)\(\Rightarrow\)MH là p/g góc BMN.
Xét \(\triangle ABC\) ta có :
\(| BC-AC| < AB < AC+BC\) ( bất đẳng thức tam giác )
\(\Rightarrow |1-7 | < AB < 1+7 \)
\(\Rightarrow |-6 | < AB < 8\)
\(\Rightarrow 6< AB < 8\)
Do \(AB \in \mathbb{Z}\) \(\Rightarrow AB = 7\)
Vậy \(AB=7\) cm .
Chọn \(\mathbb{C}\)
NMP đều cạnh 6 cm có H là giao điểm của 3 đường phân giác. Khi đó, MH có số đo là:
lx hinh kia bn
lỗi hình rồi bn ơi