Cho điểm A nằm trong góc nhọn xOy. Vẽ điểm D đối xứng với A qua Ox. Vẽ điểm E đối xứng với A qua Oy. Gọi B và C theo thứ tự là giao điểm của DE với Ox và Oy. Chứng minh rằng tam giác ABC có chu vi nhỏ nhất trong các tam giác có một đỉnh là A, hai đỉnh kia nằm trên các tia Ox và Oy.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

20 tháng 4 2016
)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC

CM
5 tháng 6 2019
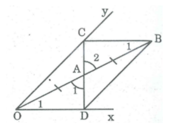
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.
