Bài 4 : ( 1,5 điểm ) : Để đo chiều rộng của một con sông AB , người ta có thể đặt hai cọc tiêu ở vị trí EF sao cho EF / AB . Chọn 1 vị trí đứng ngắm ( điểm C ) sao cho ba điểm B , E , C thẳng hàng ; ba điểm A , F , C thẳng hàng . Đo được CF = 4m , AF = 6m ; EF = 6M . Hỏi khúc sông AB đó rộng bao nhiêu mét ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 12 2023
Xét ΔCAB có FE//AB
nên \(\dfrac{CF}{FA}=\dfrac{CE}{EB}\)
=>\(\dfrac{30}{EB}=\dfrac{20}{40}=\dfrac{1}{2}\)
=>\(EB=30\cdot2=60\left(m\right)\)
14 tháng 5 2021
Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m
11 tháng 6 2021
Ta có :
\(\dfrac{NM}{AB}\) và \(\dfrac{CN}{CA}\) .
Vì \(\dfrac{NM}{AB}\) = \(\dfrac{CN}{CA}\) \(\Leftrightarrow\) AB = 1,5 . \(\dfrac{20}{1,25}\) = 24 ( m ) .
Vậy chiều cao AB của tòa nhà đó là 24 m .
1 tháng 2
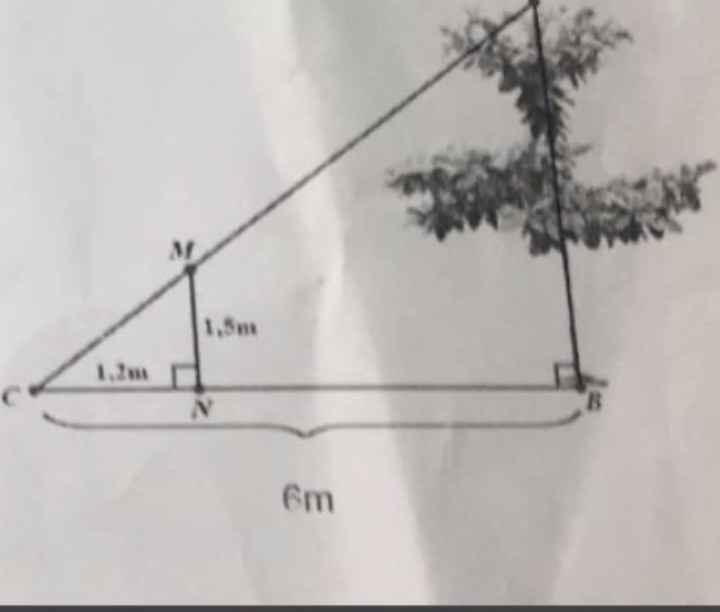
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)
8 tháng 4 2020
câu 9
a) ta có AB=6
=> AM=BM=3 cm
mà MC=AM-MC=3-2=1 cm
MD=MB-BD=3-2=1 cm
=> MC=MD
=> M là trung điểm của CD
b) C là trung điểm của AD
D là trung điểm của BC
8 tháng 4 2020
câu 10
a) AB + BO có giá trị nhỏ nhất khi và chỉ khi <=> O trùng B.
b) AB + BO = 2BO <=> AB = BO <=> O trùng A.
c) AB + BO = 3BO <=> AB = 2BO <=> O là trung điểm của AB.
Chúc bạn học tốt
Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)