Trên đường tòn (O;10cm),một dây cung cách tâm O một khoảng là 5 cm .Vayaj độ dài của dây cung là
A \(10\sqrt{3}\) B \(3\sqrt{5}\) C\(5\sqrt{3}\) D\(10\sqrt{5}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2017
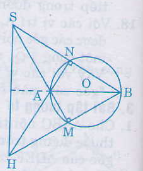
BM ⊥ SA ( =
vì là góc nội tiếp chắn nửa đường tròn).
Tương tự, có: AN ⊥ SB
Như vậy BM và AN là hai đường cao của tam giác SAB và H là trực tâm.
Suy ra SH ⊥ AB.
(Trong một tam giác ba đường cao đồng quy)
28 tháng 2 2021
a) Xét (O) có
\(\widehat{AED}\) là góc nội tiếp chắn \(\stackrel\frown{AD}\)
\(\widehat{DAM}\) là góc tạo bởi tia tiếp tuyến AM và dây cung AD
Do đó: \(\widehat{AED}=\widehat{DAM}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
\(\Leftrightarrow\widehat{AEM}=\widehat{DAM}\)
Xét ΔAEM và ΔDAM có
\(\widehat{AEM}=\widehat{DAM}\)(cmt)
\(\widehat{AMD}\) chung
Do đó: ΔAEM∼ΔDAM(g-g)
⇒\(\dfrac{ME}{MA}=\dfrac{MA}{MD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(ME\cdot MD=MA^2\)(đpcm)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAOM vuông tại A có AH là đường cao ứng với cạnh huyền AO, ta được:
\(MH\cdot MO=AM^2\)
mà \(ME\cdot MD=AM^2\)(cmt)
nên \(MD\cdot ME=MH\cdot MO\)(đpcm)
Độ dài dây cung:
\(2\sqrt{10^2-5^2}=10\sqrt{3}\)