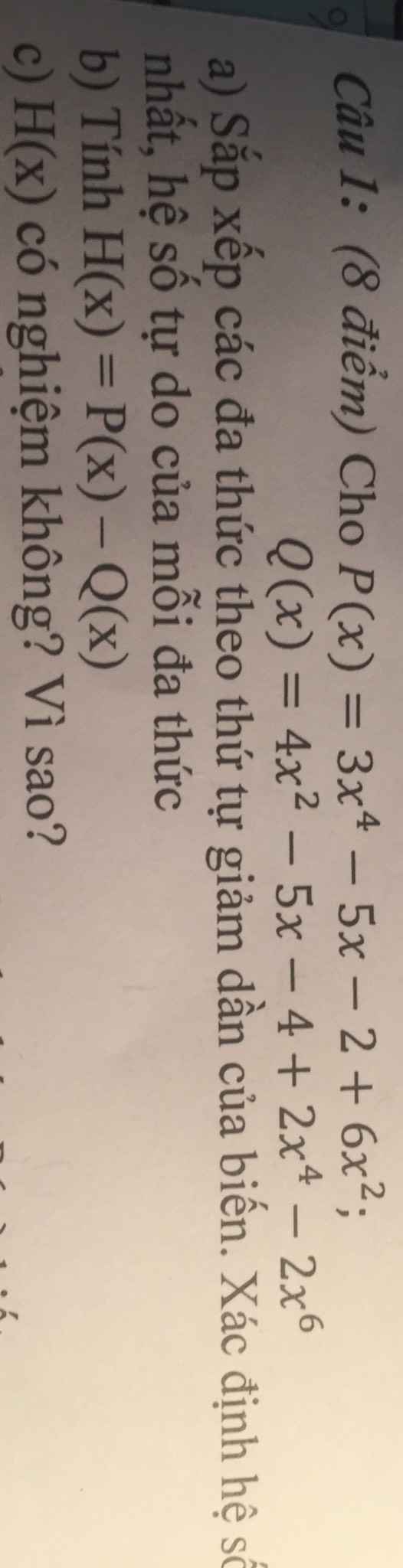
Làm giúp mình câu b với câu c với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c, \(2H_2+O_2 \rightarrow2H_2O\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5(mol) \Rightarrow n_{O_2}=0,75(mol)\)
\(V_{O_2}=22,4.0,75=16,8(l)\)
\(n_{H_2}=\dfrac{33,6}{22,4}=1,5\left(mol\right)\)
a. PTHH: \(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
Theo PTHH: \(n_{Fe}=n_{H_2}=1,5\left(mol\right)\)
\(\Rightarrow m_{Fe}=56\cdot1,5=84\left(g\right)\)
b. Đổi: \(500ml=0,5l\)
\(CM_{H_2SO_4}=\dfrac{1,5}{0,5}=3M\)
c. \(2H_2+O_2\rightarrow2H_2O\)
Theo PTHH: \(n_{O_2}=\dfrac{1}{2}n_{H_2}=\dfrac{1}{2}\cdot1,5=0,75\left(mol\right)\)
\(\Rightarrow V_{O_2}=0,75\cdot22,4=16,8\left(l\right)\)

Lời giải:
b. Tam giác $ABC$ vuông tại $A$ và $C=45^0$ nên:
$B=90^0-C=90^0-45^0=45^0$
Do đó, tam giác $ABC$ vuông cân tại $A$
$\Rightarrow AC=AB=50$ (cm)
Áp dụng định lý Pitago: $BC=\sqrt{AB^2+AC^2}=\sqrt{50^2+50^2}=50\sqrt{2}$ (cm)
f.
Theo định lý Pitago: $AC=\sqrt{BC^2-AB^2}=\sqrt{7^2-5^2}=2\sqrt{6}$ (cm)
$\sin B=\frac{AC}{BC}=\frac{2\sqrt{6}}{7}$
$\Rightarrow B=44,42^0$
$C=90^0-B=90^0-44,42^0=45,58^0$
b) Xét ΔABC vuông tại A có \(\widehat{C}=45^0\)(gt)
nên ΔABC vuông cân tại A(Định nghĩa tam giác vuông cân)
Suy ra: \(\widehat{B}=45^0\) và AC=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=50^2+50^2=5000\)
hay \(BC=50\sqrt{2}\left(cm\right)\)

a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật
b: Xét tứ giác ABQC có
M là trung điểm chung của AQ và BC
=>ABQC là hình bình hành
Hình bình hành ABQC có \(\widehat{BAC}=90^0\)
nên ABQC là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét tứ giác AMBD có
E là trung điểm chung của AB và MD
=>AMBD là hình bình hành
Hình bình hành AMBD có AB\(\perp\)MD
nên AMBD là hình thoi
d: Xét ΔABC có
M,E lần lượt là trung điểm của BC,BA
=>ME là đường trung bình cuả ΔACB
=>ME//AC và \(ME=\dfrac{AC}{2}\)
Ta có: \(ME=\dfrac{AC}{2}\)
\(ME=\dfrac{MD}{2}\)
Do đó: AC=MD
Xét tứ giác ACMD có
MD//AC
MD=AC
Do đó: ACMD là hình bình hành
=>AM cắt CD tại trung điểm của mỗi đường(1)
Ta có: AEMF là hình chữ nhật
=>AM cắt EF tại trung điểm của mỗi đường(2)
Từ (1),(2) suy ra AM,CD,EF đồng quy
c) Ta vẽ đối xứng của M qua E và gọi điểm đó là D. Khi đó, ta có:
- MD = ME (do D là đối xứng của M qua E)
- Góc MDE = 90 độ (do ME vuông góc với AB)
Vì tam giác AEMF là hình chữ nhật (theo phần a), nên ta có:
- AE = MF
- Góc EAF = 90 độ (do AE vuông góc với AB)
- Góc MFA = 90 độ (do MF vuông góc với AC)
Do đó, ta có:
- Góc EAF = Góc MFA
- AE = MF
Khi đó, ta có tứ giác AMBD là hình thoi (do MD = ME và AB song song với DE).
d) Ta cần chứng minh rằng CD, AM, EF đồng quy. Ta có:
- AM là trung tuyến của tam giác ABC, nên AM song song với BC.
- Góc MAF = 90 độ (do ME vuông góc với AB), nên góc FAE = 90 độ - góc BAC.
- Góc MFA = 90 độ (do MF vuông góc với AC), nên góc EAF = 90 độ - góc ABC.
- Tứ giác AEMF là hình chữ nhật (theo phần a), nên AE song song với MF.
Khi đó, ta có:
- Góc FAE + góc EAF = 90 độ - góc BAC + 90 độ - góc ABC = 180 độ - (góc BAC + góc ABC) = 90 độ (do tổng hai góc BAC và ABC bằng 90 độ)
- AE song song với MF
- AM song song với BC
Do đó, ta có CD, AM, EF đồng quy.


a) Do \(\dfrac{R1}{R2}=\dfrac{R3}{R4}\) nên mạch là mạch cầu cân bằng.
=> Cường độ dòng điện qua ampe kế là \(IA=0\left(A\right)\)
b) Gọi cường độ dòng điện qua các điện trở R1,R2,R3,R4 lần lượt là \(I1,I2,I3,I4\) , cường độ dòng điện qua ampe kế là \(IA'\)
Do dòng điện qua ampe kế có chiều từ M->N và có cường độ 0,2 A nên ta có:
\(I1-I3=IA'=0,2\left(A\right)\) (1)
Điện trở tương đương của mạch là:
\(Rtđ=\dfrac{R1.R2}{R1+R2}+\dfrac{R3.R4}{R3+R4}=\dfrac{10.15}{10+15}+\dfrac{12R4}{12+R4}=6+\dfrac{12R4}{12+R4}=\dfrac{72+18R4}{12+R4}\)
=> Cường độ dòng điện mạch chính là:
\(I=\dfrac{U}{Rtđ}=\dfrac{12\left(12+R4\right)}{72+18R4}=\dfrac{24+2R4}{12+3R4}\)
Cường độ dòng điện chạy qua R1 là:
\(I1=\dfrac{R2}{R1+R2}.I=\dfrac{2}{5}I\)
=>\(I3=\dfrac{R4}{R4+R3}.I=\dfrac{R4}{R4+12}I\)
=>\(IA'=\left(\dfrac{2}{5}-\dfrac{R4}{12+R4}\right)I\)
Sau đó bạn chỉ cần thay vào là tính đc nhé![]()

b: AD là phân giác
=>DB/AB=DC/AC
=>DB/DC=AB/AC=3/4
=>DB/3=DC/4
mà DB+DC=BC=14
nên DB/3=DC/4=14/7=2
=>DB=6cm; DC=8cm



a/ Pt có 2 nghiệm phân biệt
\(\to\Delta'=(-m)^2-1.(-8m-16)=m^2+8m+16=(m+4)^2>0\\\to m+4>0\quad or\quad m+4<0\\\to m>-4\quad or\quad m<-4\)
b/ Theo Vi-ét:
\(\begin{cases}x_1+x_2=2m\\x_1x_2=-8m-16\end{cases}\)
\(x_1^2+x_2^2=5\\\leftrightarrow x_1^2+2x_1x_2+x_2^2-2x_1x_2=5\\\leftrightarrow (x_1+x_2)^2-2x_1x_2=5\\\leftrightarrow (2m)^2-2.(-8m-16)=5\\\leftrightarrow 4m^2+16m+32=5\\\leftrightarrow 4(m^2+4m+8)=5\\\leftrightarrow 4(m+2)^2+16=5\\\leftrightarrow 4(m+2)^2+11=0(\text{vô lý})\\\to m\in\varnothing\)
Vậy không có giá trị m thỏa mãn
a: P(x)=3x^4+6x^2-5x-2
Q(x)=-2x^6+2x^4+4x^2-5x-4
b: H(x)=P(x)-Q(x)
=3x^4+6x^2-5x-2+2x^6-2x^4-4x^2+5x+4
=2x^6+x^4+2x^2+2
c: H(x)=x^2(2x^4+x^2+2)+2>=2>0 với mọi x
=>H(x) ko có nghiệm