Giúp e giải bài này chi tiết cảm ơn a chị 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi chiều rộng là x
Chiều dài là x+15
Theo đề, ta có phương trình:
\(\left(x+5\right)\left(x+12\right)=x\left(x+15\right)+80\)
\(\Leftrightarrow x^2+17x+60-x^2-15x=80\)
=>2x+60=80
=>x=10
Vậy: Chiều rộng là 10m
Chiều dài là 25m

Gọi độ dài quãng đường là x
Theo đề, ta có:
\(\dfrac{x}{42}-\dfrac{x}{46}=\dfrac{3}{4}\)
hay x=362,25(km)

a) Gọi số mol Fe, Zn là a, b (mol)
=> 56a + 65b = 12,1 (1)
\(n_{H_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
PTHH: Fe + 2HCl --> FeCl2 + H2
a-->2a-------->a---->a
Zn + 2HCl --> ZnCl2 + H2
b---->2b---->b------->b
=> a + b = 0,2 (2)
(1)(2) => a = 0,1 (mol); b = 0,1 (mol)
\(\left\{{}\begin{matrix}\%m_{Fe}=\dfrac{0,1.56}{12,1}.100\%=46,28\%\\\%m_{Zn}=\dfrac{0,1.65}{12,1}.100\%=53,72\%\end{matrix}\right.\)
b) nHCl = 2a + 2b = 0,4 (mol)
=> \(V_{dd.HCl}=\dfrac{0,4}{1}=0,4\left(l\right)\)
c) \(\left\{{}\begin{matrix}C_{M\left(FeCl_2\right)}=\dfrac{0,1}{0,4}=0,25M\\C_{M\left(ZnCl_2\right)}=\dfrac{0,1}{0,4}=0,25M\end{matrix}\right.\)

\(\lim\limits_{x\rightarrow5}\left(x^3+5x^2-10x+8\right)=5^3+5.5^2-10.5+8=...\)
\(\lim\limits_{x\rightarrow-2}\dfrac{x^3-x^2-2x-8}{x^2+3x+2}=\dfrac{-16}{0}=-\infty\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x^2-5x+2}{2\left|x\right|+1}=\lim\dfrac{\left|x\right|-5+\dfrac{2}{\left|x\right|}}{2+\dfrac{1}{\left|x\right|}}=\dfrac{+\infty}{2}=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt[3]{x^3+4x-3}-4x}{\sqrt{9x^2-5x+1}-4x}=\lim\limits_{x\rightarrow+\infty}\dfrac{x\left(\sqrt[3]{1+\dfrac{4}{x^2}-\dfrac{3}{x^3}}-4\right)}{x\left(\sqrt[]{9-\dfrac{5}{x}+\dfrac{1}{x^2}}-4\right)}=\dfrac{1-4}{3-4}=3\)
Lời giải:
a.
\(\lim\limits_{x\to 5}(x^3+5x^2-10x+8)=5^3+5.5^2-10.5+8=208\)
b.
\(L=\lim\limits_{x\to -2}\frac{x^3-x^2-2x-8}{x^2+3x+2}\lim\limits_{x\to -2}\frac{x^3-x^2-2x-8}{x+1}.\frac{1}{x+2}=16\lim\limits_{x\to -2}\frac{1}{x+2}\)\(\lim\limits_{x\to -2-}\frac{1}{x+2}=-\infty \Rightarrow L=-\infty ; \lim\limits_{x\to -2+}\frac{1}{x+2}=+\infty \Rightarrow L=+\infty \)


3:
1: Gọi tuổi mẹ và tuổi con hiện nay lần lượt là x,y
Theo đề, ta có: x=2,3y và x-16=7,5(y-16)
=>x-2,3y=0 và x-7,5y=-120+16=-104
=>x=46 và y=20
Gọi số năm nữa để tuổi mẹ gấp đôi tuổi con là a
Theo đề, ta có
a+46=2a+40
=>-a=-6
=>a=6
2:
Xe đi 210m trong 30-16=14s
=>V=210/14=15m/s
Chiều dài là:
15*16=240(m)

bài 1
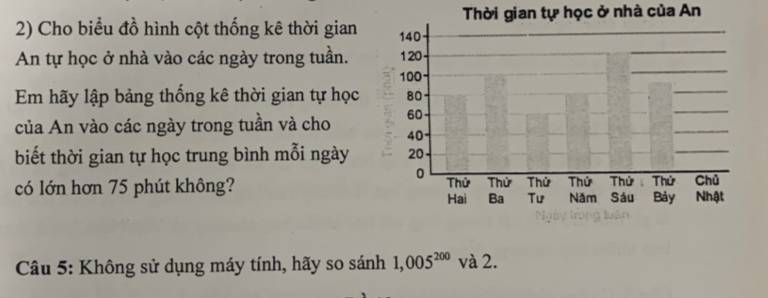
| thứ | 2 | 3 | 4 | 5 | 6 | 7 | CN |
| TG học | 80p | 100p | 60p | 80p | 120p | 90p | 0p |
TBC TG bạn học 1 ngày là : (80*2+100+60+120+90+0)/7 \(\approx\) 76
Vậy TG bạn học 1 ngày là hơn 75p
2
ko bt nhưng chắc chắn là 1,005200
LỚN HƠN NHA

3:
1: Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có: 6/5a*4/5b=ab-30
=>ab=750
=>S=750
2:
Sau 1,5h thì xe 1 đi được 15*1,5=22,5(km)
Hiệu vận tốc là 20-15=5(km/h)
Thời gian hai xe đuổi kịp nhau là:
22,5/5=4,5(h)
=>Người 1 đi đến B sau 5h
ĐỘ dài AB là:
15*5=75km



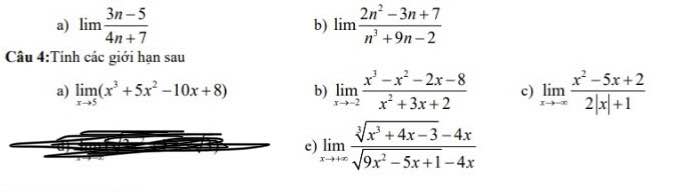




Gọi kim loại cần tìm là R (II)
Gọi \(\left\{{}\begin{matrix}n_{Fe}=a\left(mol\right)\\n_R=b\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow56a+M_R.b=8\left(g\right)\)
\(n_{HCl}=0,2.2=0,4\left(mol\right)\)
PTHH:
Fe + 2HCl --->FeCl2 + H2
a---->2a
R + 2HCl ---> RCl2 + H2
b---->2b
Theo pthh: \(n_{hhkl}=n_{H_2}=\dfrac{1}{2}n_{HCl}=\dfrac{1}{2}.0,4=0,2\left(mol\right)\)
\(\Rightarrow V_{H_2}=0,2.22,4=4,48\left(l\right)\)
b, Lập được hệ pt: \(\left\{{}\begin{matrix}56a+M_R.b=8\\2a+2b=0,4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0,1\left(mol\right)\\b=0,1\left(mol\right)\\M_R=24\left(\dfrac{g}{mol}\right)\end{matrix}\right.\)
=> R là Mg
c, \(\left\{{}\begin{matrix}n_{Fe}=0,1\left(mol\right)\\n_{Mg}=0,1\left(mol\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m_{Fe}=0,1.56=5,6\left(g\right)\\m_{Mg}=0,1.56=5,6\left(g\right)\end{matrix}\right.\)
Quy hết kim loại R (II) và Fe về M (II):
\(n_{HCl}=0,2.2=0,4\left(mol\right)\)
PTHH: M + 2HCl ---> MCl2 + H2↑
0,2<-0,4------->0,2---->0,2
=> VH2 = 0,2.22,4 = 4,48 (l)
\(b,M_M=\dfrac{8}{0,2}=40\left(\dfrac{g}{mol}\right)\\ \rightarrow M_R=2.40-56=24\left(\dfrac{g}{mol}\right)\)
=> R là Mg
c, Gọi \(\left\{{}\begin{matrix}n_{Fe}=a\left(mol\right)\\n_{Mg}=b\left(mol\right)\end{matrix}\right.\left(a,b>0\right)\)
PTHH:
Fe + 2HCl ---> FeCl2 + H2
a---->2a--------->a
Mg + 2HCl ---> MgCl2 + H2
b---->2b-------->b
=> hệ pt \(\left\{{}\begin{matrix}56a+24b=8\\2a+2b=0,4\end{matrix}\right.\Leftrightarrow a=b=0,1\left(mol\right)\left(TM\right)\)
=> \(\left\{{}\begin{matrix}m_{Fe}=0,1.56=5,6\left(g\right)\\m_{Mg}=0,1.24=2,4\left(g\right)\end{matrix}\right.\)
d, \(\left\{{}\begin{matrix}C_{M\left(FeCl_2\right)}=\dfrac{0,1}{0,2}=0,5M\\C_{M\left(MgCl_2\right)}=\dfrac{0,1}{0,2}=0,5M\end{matrix}\right.\)