tìm k lớn nhất thỏa mãn (x2+x).(x2+11x+30)+7 ≥k với mọi x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2021
PT có 2 nghiệm \(\Leftrightarrow\Delta'=\left(k-2\right)^2-\left(-2k-5\right)\ge0\)
\(\Leftrightarrow k^2-4k+4+2k+10\ge0\\ \Leftrightarrow k^2-2k+14\ge0\\ \Leftrightarrow k\in R\)
Vậy PT luôn có 2 nghiệm
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(k-2\right)\left(1\right)\\x_1x_2=-2k-5\left(2\right)\end{matrix}\right.\)
Lại có \(2x_1-x_2=7\left(3\right)\)
\(\left(1\right)\left(3\right)\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\left(k-2\right)\\2x_1-x_2=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x_1=2k+3\\x_2=2x_1-7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{2k+3}{2}\\x_2=\dfrac{4k+6}{2}-7=\dfrac{4k-8}{2}=2k-4\end{matrix}\right.\)
Thay vào \(\left(2\right)\Leftrightarrow\dfrac{\left(2k+3\right)\left(2k-4\right)}{2}=-2k-5\)
\(\Leftrightarrow\left(2k+3\right)\left(k-2\right)=-2k-5\\ \Leftrightarrow2k^2-k-6+2k+5=0\\ \Leftrightarrow2k^2+k-1=0\\ \Leftrightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-1\end{matrix}\right.\)
6 tháng 2 2022
Xét pt :
\(x^2-2\left(k+2\right)x+k^2+2k-7=0\)
\(\Delta'=\left(k+2\right)^2-\left(k^2+2k-7\right)\)
\(=k^2+4k+4-k^2-2k+7\)
\(=2k+11\)
Để phương trình có 2 nghiệm pb \(\Leftrightarrow k>-\dfrac{11}{2}\)
Theo định lí Viet ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(k+2\right)\\x_1.x_2=k^2+2k-7\end{matrix}\right.\)
Ta có :
\(x_1^2+x_2^2=x_1.x_2+28\)
\(\Leftrightarrow\left(x_1+x_2\right)^2=3x_1.x_2+28\)
\(\Leftrightarrow4\left(k+2\right)^2=3\left(k^2+2k-7\right)+28\)
Tự giải hết pt tìm k nhé :> Buồn ngủ quá ~
5 tháng 2 2022
a: Thay k=-3 vào pt, ta được:
\(x^2-2\cdot\left(-3+2\right)x+\left(-3\right)^2+2\cdot\left(-3\right)-7=0\)
\(\Leftrightarrow x^2+2x-4=0\)
\(\Leftrightarrow\left(x+1\right)^2=5\)
hay \(x\in\left\{\sqrt{5}-1;-\sqrt{5}-1\right\}\)
b: \(\text{Δ}=\left(2k+4\right)^2-4\left(k^2+2k-7\right)\)
\(=4k^2+16k+16-4k^2-8k+28\)
=8k+44
Để phương trình có hai nghiệm thì 8k+44>=0
=>8k>=-44
hay k>=-11/2
Theo đề, ta có: \(\left(x_1+x_2\right)^2-3x_1x_2=28\)
\(\Leftrightarrow\left(2k+4\right)^2-3\cdot\left(k^2+2k-7\right)=28\)
\(\Leftrightarrow4k^2+16k+16-3k^2-6k+21=28\)
\(\Leftrightarrow k^2+10k+37-28=0\)
\(\Leftrightarrow\left(k+1\right)\left(k+9\right)=0\)
=>k=-1
25 tháng 5 2021
A, B thuộc (P), (d) ?
Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=k\left(x-1\right)+2\Leftrightarrow x^2-kx+\left(k-2\right)=0\).
Ta có \(\Delta=k^2-4\left(k-2\right)=\left(k-2\right)^2+2>0\forall k\) nên phương trình trên luôn có hai nghiệm phân biệt.
Theo hệ thức Viète ta có \(\left\{{}\begin{matrix}x_1x_2=k-2\\x_1+x_2=k\end{matrix}\right.\).
Ta có \(x_1^2+y_1+x_2^2+y_2=14\)
\(\Leftrightarrow2x_1^2+2x_2^2=14\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=7\)
\(\Leftrightarrow k^2-2\left(k-2\right)=7\Leftrightarrow k^2-2k-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=-1\\k=3\end{matrix}\right.\).
Vậy...
15 tháng 7 2019
1) \(x^2-2mx+m-2=0\) (1)
pt (1) có \(\Delta'=\left(-m\right)^2-\left(m-2\right)=m^2-m+2=\left(m-\frac{1}{2}\right)^2+\frac{7}{4}>0\left(\forall m\right)\)
=> pt luôn có 2 nghiệm phân biệt x1, x2
Vi-et: \(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=m-2\end{cases}}\)\(\Rightarrow\)\(M=\frac{2x_1x_2-\left(x_1+x_2\right)}{x_1^2+x_2^2-6x_1x_2}=\frac{2x_1x_2-\left(x_1+x_2\right)}{\left(x_1+x_2\right)^2-8x_1x_2}=\frac{2m-4-2m}{\left(2m\right)^2-8m-16}\)
\(=\frac{-4}{4m^2-8m-16}=\frac{-4}{4\left(m-1\right)^2-20}\ge\frac{-4}{-20}=\frac{1}{5}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(m=1\)
xin 1slot sáng giải
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2020
1.
\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)
\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)
\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)
\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)
Đặt \(xy=a\Rightarrow0< a\le1\)
\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)
\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)
\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)
\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)
\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)
\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)
Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2020
2.
Đặt \(A=9^n+62\)
Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)
Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)
\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)
Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\) và \(6m+1\)
\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)
\(\Leftrightarrow36m^2=9^n+63\)
\(\Leftrightarrow4m^2=9^{n-1}+7\)
\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)
\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)
Pt ước số cơ bản, bạn tự giải tiếp
CM
27 tháng 6 2019
7 x 2 (x – 7) + 5x(7 – x) = 0
ó 7x.x(x – 7) – 5.x(x – 7) = 0
ó (7x.x – 5.x)(x – 7) = 0
ó x(7x – 5)(x – 7) = 0
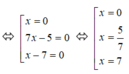
Giá trị lớn nhất của x thỏa mãn đề bài là x = 7.
Đáp án cần chọn là: B
17 tháng 2 2020
Theo c) \(f\left(\frac{5}{7}\right)=f\left(\frac{2}{7}+\frac{3}{7}\right)=f\left(\frac{2}{7}\right)+f\left(\frac{3}{7}\right)\)
\(f\left(\frac{2}{7}\right)=f\left(\frac{1}{7}+\frac{1}{7}\right)=f\left(\frac{1}{7}\right)+f\left(\frac{1}{7}\right)=2.f\left(\frac{1}{7}\right)\)
\(f\left(\frac{3}{7}\right)=f\left(\frac{1}{7}+\frac{2}{7}\right)=f\left(\frac{1}{7}\right)+f\left(\frac{2}{7}\right)=f\left(\frac{1}{7}\right)+2f\left(\frac{1}{7}\right)=3.f\left(\frac{1}{7}\right)\)
\(\implies\)\(f\left(\frac{5}{7}\right)=5.f\left(\frac{1}{7}\right)\) (1)
Theo b) \(f\left(\frac{1}{7}\right)=\frac{1}{7^2}.f\left(7\right)\) (2)
Theo c) \(f\left(7\right)=f\left(3+4\right)=f\left(3\right)+f\left(4\right)\)
\(=2.f\left(3\right)+f\left(1\right)\)
\(=6.f\left(1\right)+f\left(1\right)\)
\(=7.f\left(1\right)\)
Theo a)\(f\left(1\right)=1\)\(\implies\)\(f\left(7\right)=7\) (3)
Từ (1);(2);(3)
\(\implies\) \(f\left(\frac{5}{7}\right)=\frac{5}{7}\)
Lời giải:
$(x^2+x)(x^2+11x+30)+7=x(x+1)(x+5)(x+6)+7$
$=(x^2+6x)(x^2+6x+5)+7$
$=(x^2+6x)^2+5(x^2+6x)+7$
$=(x^2+6x+\frac{5}{2})^2+\frac{3}{4}\geq \frac{3}{4}$ với mọi $x\in\mathbb{R}$
Do đó $\frac{3}{4}\geq k$ nên $k_{\max}=\frac{3}{4}$