Giải hộ với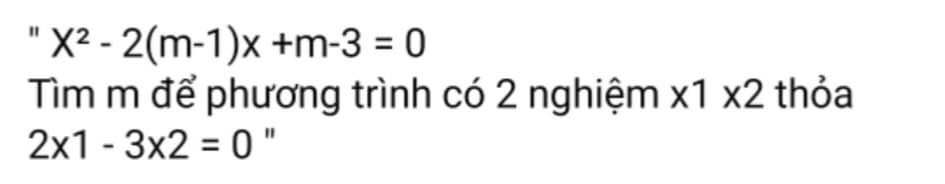
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
2
S
14 tháng 3 2023
\(\dfrac{19}{20}-x=\dfrac{8}{5}+\dfrac{3}{4}\)
\(\dfrac{19}{20}-x=\dfrac{32}{20}+\dfrac{15}{20}\)
\(\dfrac{19}{20}-x=\dfrac{47}{20}\)
\(x=\dfrac{19}{20}-\dfrac{47}{20}\)
\(x=\dfrac{-28}{20}=\dfrac{-7}{5}\)
| #DatNe |
HP
7 tháng 9 2021
5.
\(sin\left(60^o+2x\right)=-1\)
\(\Leftrightarrow60^o+2x=-90^o+k.360^o\)
\(\Leftrightarrow x=-75^o+k.180^o\)
6.
\(sin\left(2x+1\right)=\dfrac{1}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=arcsin\dfrac{1}{3}+k2\pi\\2x+1=\pi-arcsin\dfrac{1}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}arcsin\dfrac{1}{3}-\dfrac{1}{2}+k\pi\\x=\dfrac{\pi}{2}-\dfrac{1}{2}arcsin\dfrac{1}{3}-\dfrac{1}{2}+k\pi\end{matrix}\right.\)
7 tháng 9 2021
Cách làm :
sina = \(\dfrac{1}{2}\) ⇔ \(\left[{}\begin{matrix}a=\dfrac{\pi}{6}+k2\pi\\a=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
sina = \(-\dfrac{\sqrt{3}}{2}\) ⇔ \(\left[{}\begin{matrix}a=-\dfrac{\pi}{3}+k2\pi\\a=\dfrac{4\pi}{3}+k2\pi\end{matrix}\right.\)
sina = 1 ⇔ \(a=\dfrac{\pi}{2}+k.2\pi\)
sina = 0 ⇔ \(a=k\pi\)
sina = -1 ⇔ \(a=-\dfrac{\pi}{2}+k.2\pi\)
sina = \(\dfrac{1}{3}\) ⇔ \(\left[{}\begin{matrix}a=arcsin\left(\dfrac{1}{3}\right)+k2\pi\\a=\pi-arcsin\left(\dfrac{1}{3}\right)+k2\pi\end{matrix}\right.\)
Với a là một đa thức xác định trên R
KK
5 tháng 9 2021
H1: x = 360o - 130o - 60o - 82o = 88o
H2: x = 360o - 90o - 90o - 72o = 108o
H3: x = 360o - 90o - 115o - 70o = 85o
H4: 2x = 360o - 71o - 105o = 184o
=> x = 184o : 2 = 62o
AH
Akai Haruma
Giáo viên
21 tháng 5 2022
Lời giải:
Gọi $I(a,b)$ là tâm đường tròn
$(I)$ tiếp xúc với $(d)$ nên: \(R=d(I,(d))=\frac{|a-b+1|}{\sqrt{2}}(*)\)
Mặt khác:
\(\overrightarrow{AB}=(6,-2)\)
\(H(9,4)\) là trung điểm $AB$. \(\overrightarrow{HI}=(a-9,b-4)\)
\(\overrightarrow{HI}\perp \overrightarrow{AB}\Rightarrow 6(a-9)-2(b-4)=0\)
\(\Leftrightarrow 3a-b=23\)
Thay vô $(*)$ thì $R=\frac{|24-2a|}{\sqrt{2}}$
Ta cũng có \(R=IA=\sqrt{(a-6)^2+(b-5)^2}=\sqrt{(a-6)^2+(3a-23-5)^2}\)
\(=\sqrt{10a^2-180a+820}\)
Vậy: \(\frac{|24-2a|}{\sqrt{2}}=\sqrt{10a^2-180a+820}\)
$\Leftrightarrow (24-2a)^2=2(10a^2-180a+820)$
$\Leftrightarrow 16a^2-264a+1064=0$
$\Leftrightarrow 2a^2-33a+133=0$
$\Leftrightarrow a=\frac{19}{2}$ hoặc $a=7$
Đến đây bạn tìm được tâm hình tròn, biết bán kính thì sẽ tìm được pt đường tròn.
DT
Đỗ Thanh Hải
CTVVIP
6 tháng 5 2021
9 C
10 A
11 A
12 C
13 B
14 D
15 C
16 D
17 A
18 D
19 B
20 C
21 A
22 A
23 B
24 B
B
1 In spite of being young, she performs excellently
2 The problen of energy shortage will be solved by using solar energy
Ta có: \(\Delta=\left[-2\left(m-1\right)\right]^2-4\cdot1\cdot\left(m-3\right)\)
\(=\left(2m-2\right)^2-4\left(m-3\right)\)
\(=4m^2-8m+4-4m+12\)
\(=4m^2-12m+16\)
\(=4m^2-2\cdot2m\cdot3+9+7\)
\(=\left(2m-3\right)^2+7>0\forall x\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)=2m-2\\x_1\cdot x_2=m-3\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\2x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=4m-4\\2x_1-3x_2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x_2=4m-4\\x_1=2m-2-x_2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{4m-4}{5}\\x_1=\dfrac{10m-10-4m+4}{5}=\dfrac{6m-6}{5}\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=m-3\)
\(\Leftrightarrow\dfrac{4m-4}{5}\cdot\dfrac{6m-6}{5}=m-3\)
\(\Leftrightarrow\left(4m-4\right)\left(6m-6\right)=25\left(m-3\right)\)
\(\Leftrightarrow24m^2-24m-24m+24=25m-75\)
\(\Leftrightarrow24m^2-48m+24-25m+75=0\)
\(\Leftrightarrow24m^2-73m+99=0\)(1)
\(\Delta=\left(-73\right)^2-4\cdot24\cdot99=-4175< 0\)
Suy ra: Phương trình (1) vô nghiệm
Vậy: Không có giá trị nào của m để phương trình \(x^2-2\left(m-1\right)x+m-3=0\) có hai nghiệm phân biệt thỏa mãn \(2x_1-3x_2=0\)