Giúp mình bài 7 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 10 2021
Bài 6:
a: \(\sqrt{\dfrac{2}{3-\sqrt{5}}}=\dfrac{\sqrt[4]{2}\cdot\left(\sqrt[2]{5}+1\right)}{2}\)
b: \(\sqrt{\dfrac{a-4}{2\left(\sqrt{a}-2\right)}}=\dfrac{\sqrt{2}\left(\sqrt{a}+2\right)}{2}\)
BH
1
29 tháng 1
Bài 7:
a: ĐKXĐ: \(x\notin\left\{\dfrac{1}{2};-5\right\}\)
\(\dfrac{x+5}{2x-1}-\dfrac{1-2x}{x+5}-2=0\)
=>\(\dfrac{x+5}{2x-1}+\dfrac{2x-1}{x+5}-2=0\)
=>\(\dfrac{\left(x+5\right)^2+\left(2x-1\right)^2}{\left(2x-1\right)\left(x+5\right)}=2\)
=>\(\left(x+5\right)^2+\left(2x-1\right)^2=2\left(2x-1\right)\left(x+5\right)\)
=>\(x^2+10x+25+4x^2-4x+1=2\left(2x^2+10x-x-5\right)\)
=>\(5x^2+6x+26-4x^2-18x+10=0\)
=>\(x^2-12x+36=0\)
=>\(\left(x-6\right)^2=0\)
=>x-6=0
=>x=6(nhận)
b: ĐKXĐ: \(x\notin\left\{3;-2;4\right\}\)
\(1-\dfrac{8}{x-4}=\dfrac{5}{3-x}-\dfrac{8-x}{x+2}\)
=>\(\dfrac{x-4-8}{x-4}=\dfrac{-5}{x-3}+\dfrac{x-8}{x+2}\)
=>\(\dfrac{x-12}{x-4}=\dfrac{-5\left(x+2\right)+\left(x-8\right)\left(x-3\right)}{\left(x-3\right)\left(x+2\right)}\)
=>\(\dfrac{x-12}{x-4}=\dfrac{-5x-10+x^2-11x+24}{\left(x-3\right)\left(x+2\right)}\)
=>\(\left(x-12\right)\left(x^2-x-6\right)=\left(x-4\right)\left(x^2-16x+14\right)\)
=>\(x^3-x^2-6x-12x^2+12x+72=x^3-16x^2+14x-4x^2+64x-56\)
=>\(-13x^2+6x+72=-20x^2+78x-56\)
=>\(7x^2-72x+128=0\)
=>\(\left[{}\begin{matrix}x=8\left(nhận\right)\\x=\dfrac{16}{7}\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x-1}{x+2}+\dfrac{2}{x-2}=\dfrac{12}{x^2-4}\)
=>\(\dfrac{x-1}{x+2}+\dfrac{2}{x-2}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}\)
=>\(\dfrac{\left(x-1\right)\left(x-2\right)+2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}\)
=>\(x^2-3x+2+2x+4=12\)
=>\(x^2-x-6=0\)
=>(x-3)(x+2)=0
=>\(\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
16 tháng 11 2021
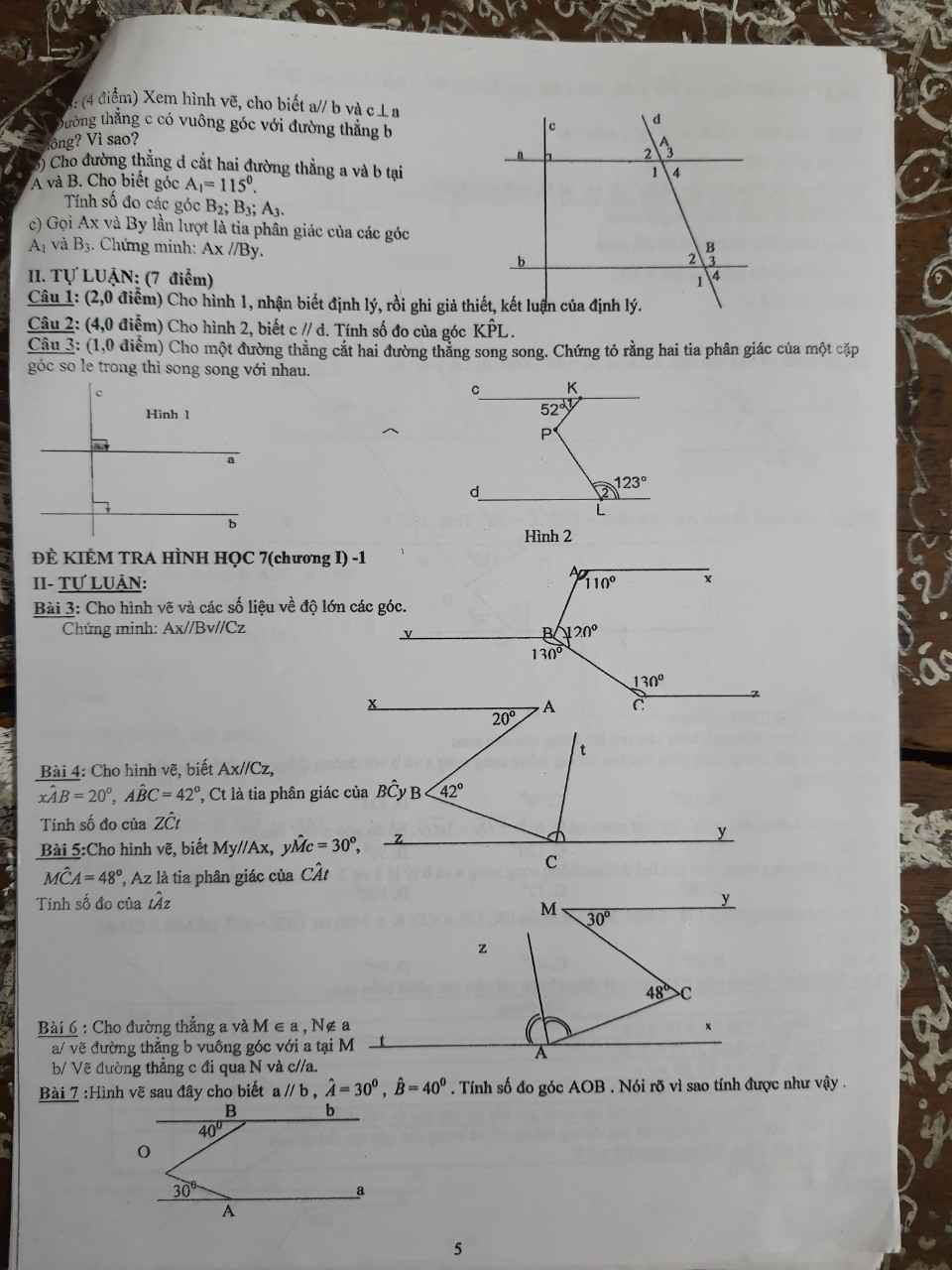
Bài 7:
\(\widehat{AOB}+\widehat{A}+\widehat{B}=360^0\)
nên Ax//By
giúp mình bài 7, bài 8 với ạ, cảm ơn nhiều
TP
12 tháng 7 2021
7. a) Hợp chất X của A với C: ACx
Ta có: \(\dfrac{A}{A+12x}.100=62,5\)
Lập bảng:
| x | 1 | 2 | 3 |
| A | 20 | 40 | 60 |
| Kết luận | Loại | Chọn (Ca) | Loại |
Vậy nguyên tố A là Ca
CTPT của hợp chất X : CaC2
CTCT:
b)Gọi số oxh của C trong chất là x. Ta có số oxh của Ca là +2
Trong CaC2: 2 + 2. x = 0 → x = -1
Số oxh của C trong CaC2 là -1
Xét phương trình \(x^2-2mx+2m-2=0\)
\(\Delta'=m^2-2m+2>0,\forall m\) nên phương trình luôn có hai nghiệm phân biệt \(x_1,x_2\).
Áp dụng hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m-2\end{matrix}\right.\)
Để \(x_1+3x_2=6\) thì \(\left\{{}\begin{matrix}x_1+3x_2=6\\x_1+x_2=2m\\x_1x_2=2m-1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x_2=6-2m\\x_1=2m-x_2\\x_1x_2=2m-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=3-m\\x_1=3m-3\\x_1x_2=2m-1\end{matrix}\right.\)\(\Rightarrow\left(3-m\right)\left(3m-3\right)=2m-1\)
\(\Rightarrow-3m^2+10m-8=0\Rightarrow\left[{}\begin{matrix}m=2\\m=\dfrac{4}{3}\end{matrix}\right.\)