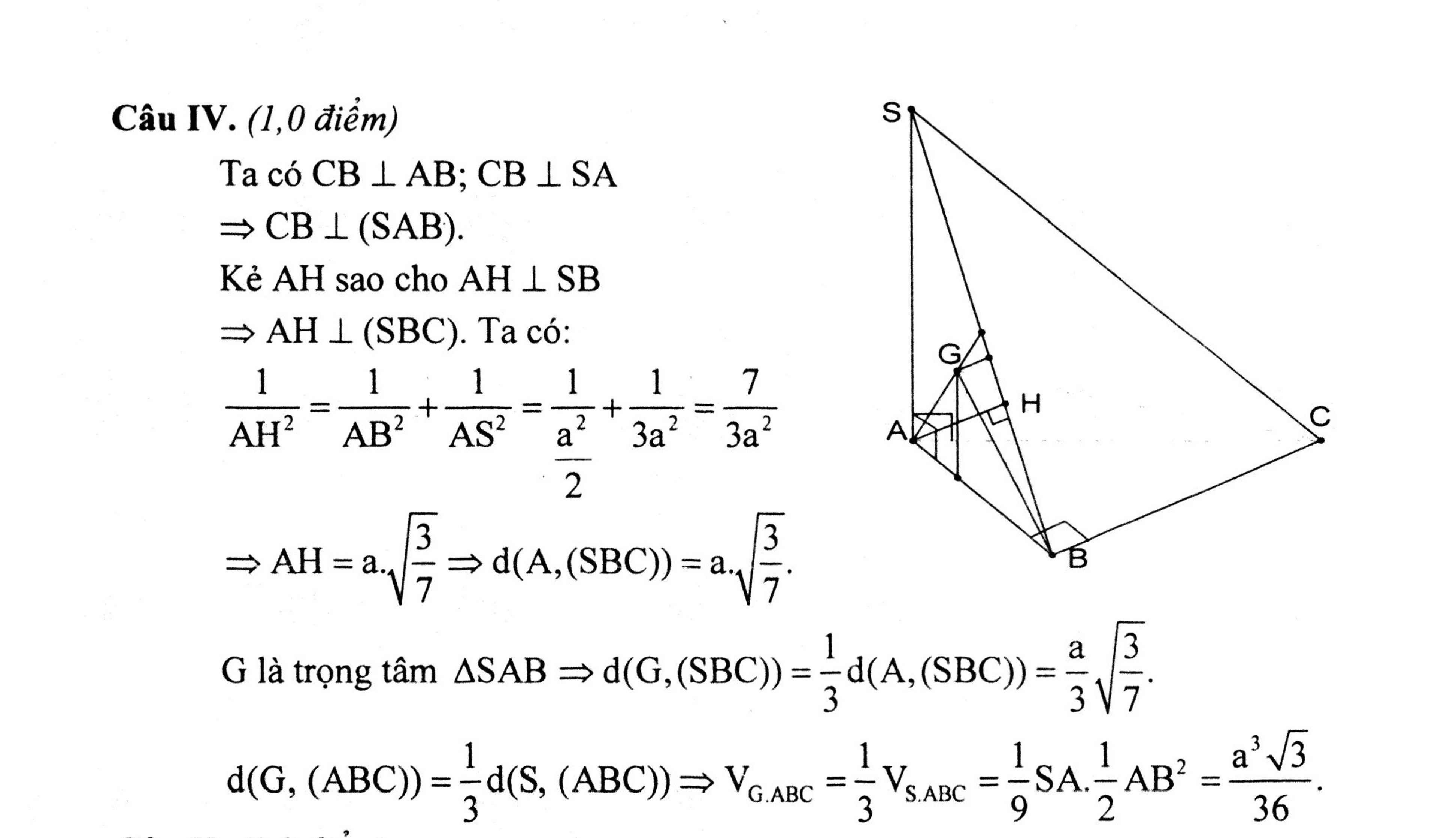
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại B. Cạnh AB=a . SA vuônh góc với (ABC) , SA=a căn 2 Gọi G là trọng tâm tam giác ABC. Tính (G,(SAB))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
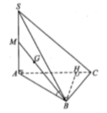
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)
CM
25 tháng 8 2017
Đáp án B
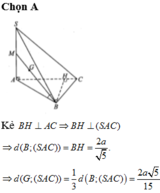
Gọi H là chân đường vuông góc hạ từ đỉnh S lên mặt phẳng (ABC), khi đó ta chứng minh được H là trung điểm của BC. Gọi M là trung điểm của AB khi đó từ giả thiết ta có: 
Đặt AB = x ta tính được: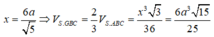 
12 tháng 5 2023
a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ
CM
28 tháng 3 2019
Phương pháp:
+) Gọi M, N, P, Q lần lượt là trung điểm của AB, SC, BC, AC. Chứng minh ∠ S A ; B C = ∠ N Q ; M Q
+) Áp dụng định lí cosin trong tam giác MNQ.
Cách giải:
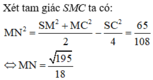
Áp dụng định lý cosin trong tam giác MNQ:
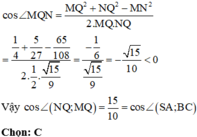
Chú ý: Góc giữa hai đường thẳng là góc nhọn nên cosin của góc giữa hai đường thẳng là giá trị dương.
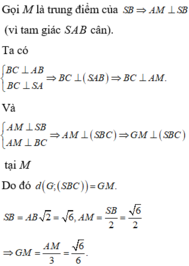
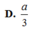
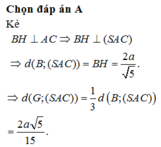
tham khảo
refẻr\