Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

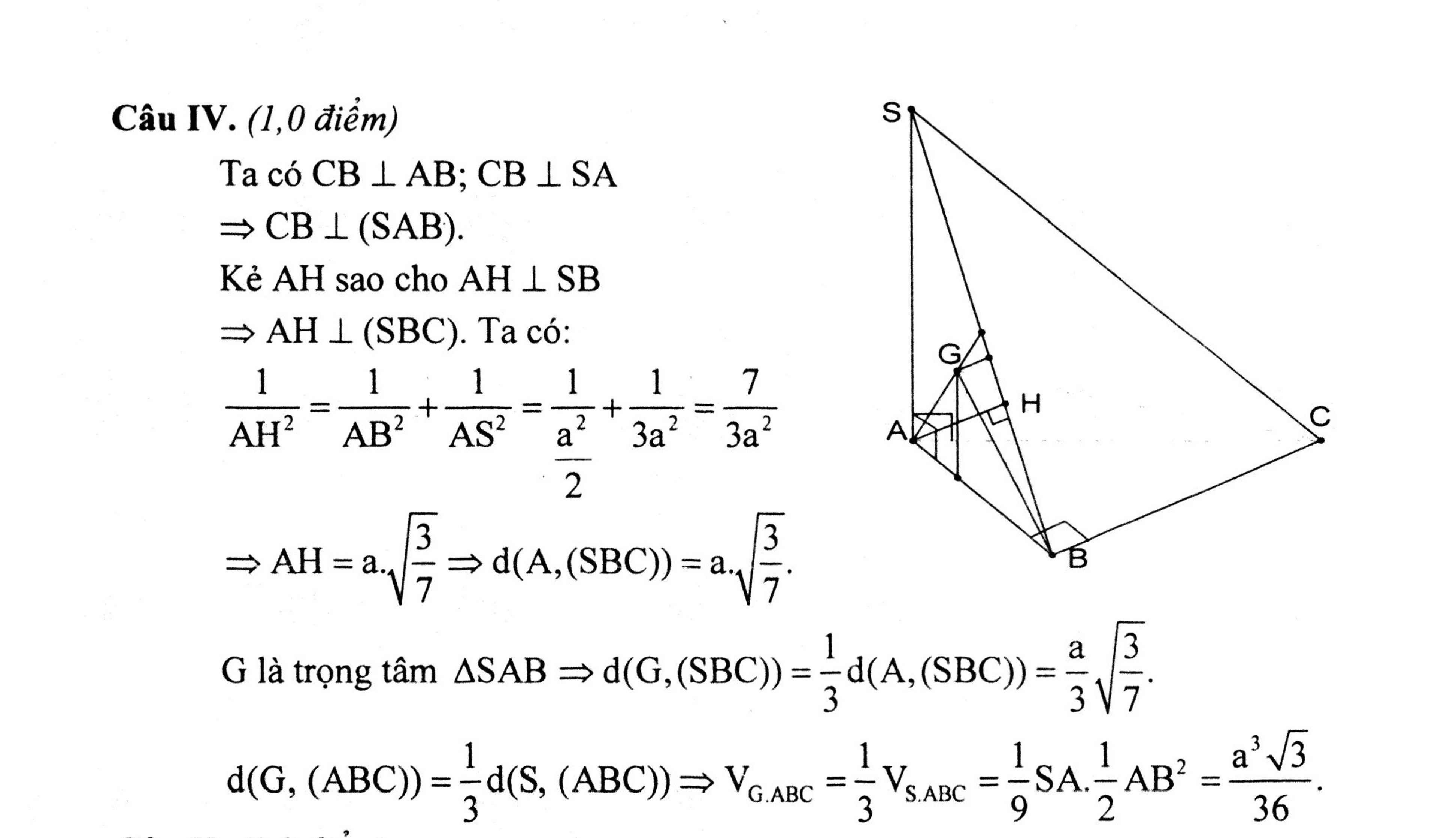
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\)
Gọi D là trung điểm AB, theo tính chất trọng tâm: \(GD=\dfrac{1}{3}CD\)
\(\Rightarrow d\left(G;\left(SAB\right)\right)=\dfrac{1}{3}d\left(C;\left(SAB\right)\right)=\dfrac{1}{3}BC=\dfrac{1}{3}AB=\dfrac{a}{3}\)

a: SO vuông góc (ABC)
=>(SGO) vuông góc (ABC)
b: ((SAB);(ABC))=(SG;AG)=góc SGA
\(AG=\dfrac{a\sqrt{3}}{3}\)
cos SGA=AG/SA=căn 3/3:2=căn 3/6
=>góc SGA=73 độ

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: Kẻ AK vuông góc SM
=>AK=d(A;(SBC))
AM=4a*căn 3/2=2a*căn 3
=>SM=4a
=>AK=2a*2a*căn 3/4a=a*căn 3

a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow BC\perp\left(SAB\right)\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\BH\in\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow SA\perp BH\)
Lại có \(BH\perp AC\) (do BH là đường cao)
\(\Rightarrow BH\perp\left(SAC\right)\)
Mà \(SC\in\left(SAC\right)\)
\(\Rightarrow BH\perp SC\)
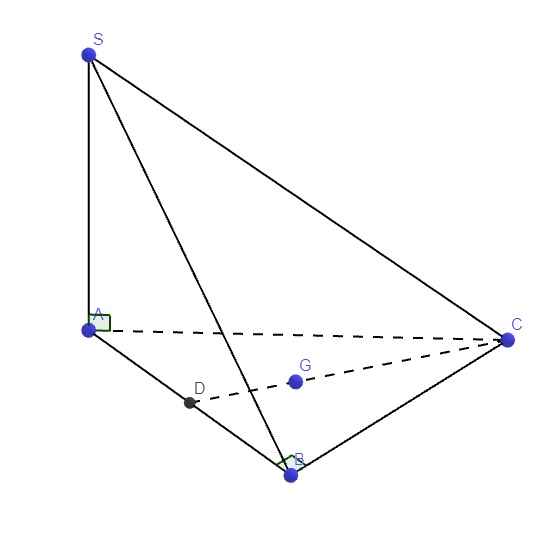

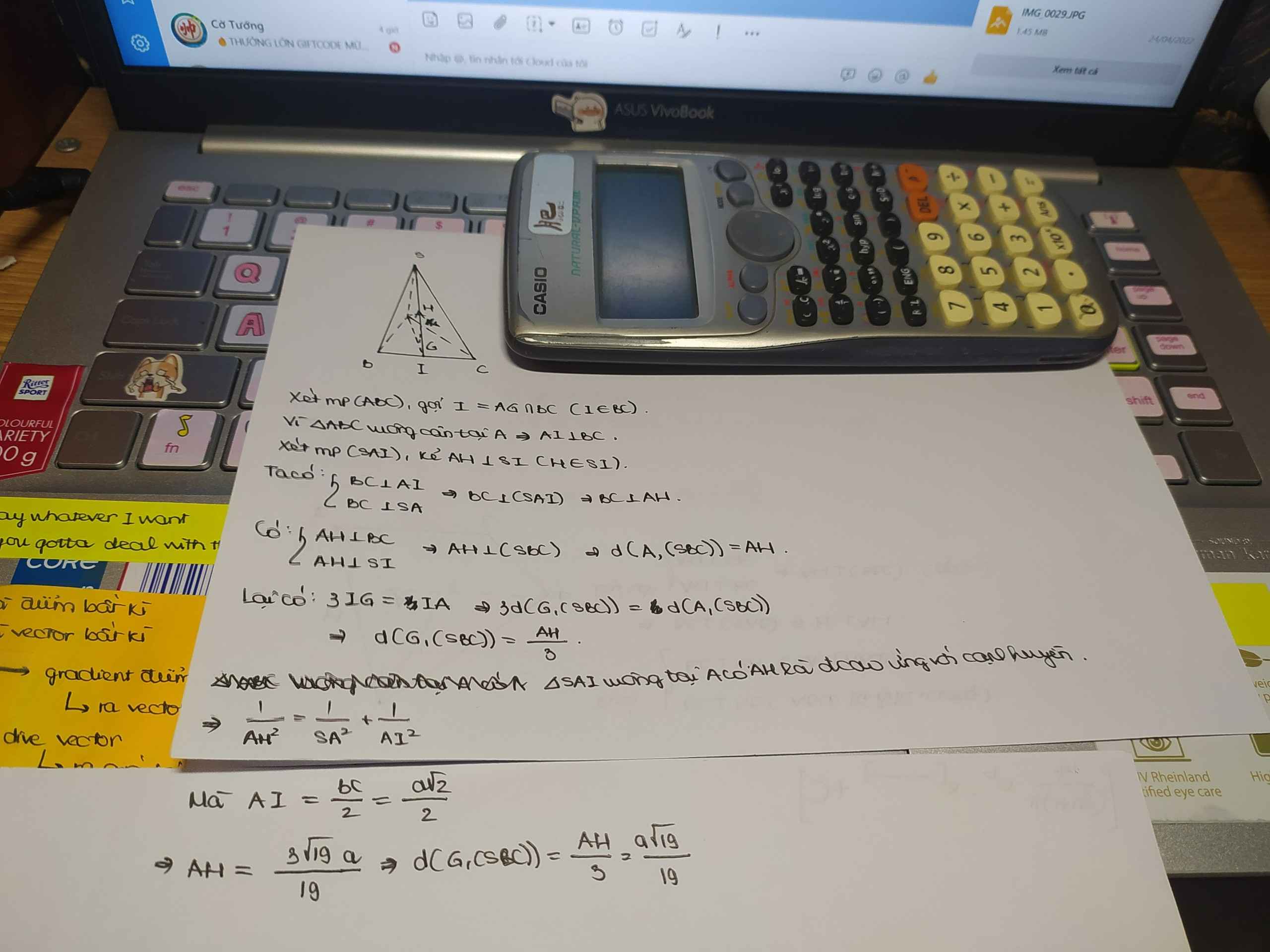
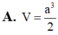
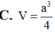
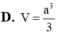
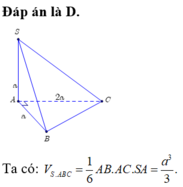
tham khảo
refẻr\