1.Cho hình chóp S.ABC có \(\Delta ABC\) vuông cân tại C có AC=a
\(SA\perp\left(ABC\right)\) và \(SA=a\sqrt{3}\)
a) Tính góc giữa \(SB\) và (ABC), SB và (SAC)
b) Tính góc giữa 2 mặt phẳng (SBC) và (ABC), (SAC) và (ABC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M là trung điểm BC \(\Rightarrow AM\perp BC\) (trung tuyến đống thời là đường cao)
Mà \(SA\perp\left(ABC\right)\Rightarrow SA\perp BC\)
\(\Rightarrow BC\perp\left(SAM\right)\)
Trong tam giác vuông SAM, kẻ đường cao \(AH\perp SM\)
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow\widehat{ASH}\) hay \(\widehat{ASM}\) là góc giữa SA và (SBC)
\(AM=\dfrac{1}{2}BC=\dfrac{1}{2}AB\sqrt{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{ASM}=\dfrac{AM}{SA}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{ASM}\approx35^016'\)

a: (SB;(ABC))=(BS;BA)=góc SBA
BA^2+BC^2=AC^2
=>2*BA^2=AC^2
=>AB=BC=a
tan SBA=SA/SB=căn 3
=>góc SBA=60 độ
d: (SB;(BAC))=(BS;BA)=góc SBA=60 độ
e:
CB vuông góc AB
CB vuông góc SA
=>CB vuông góc (SBA)
=>(SC;(SBA))=(SC;SB)=góc BSC
SB=căn SA^2+AB^2=2a
SC=căn SA^2+AC^2=a*căn 5
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
sin BSC=BC/SC=a/a*căn 5=1/căn 5
=>góc BSC\(\simeq27^0\)

a: AC vuông góc SB
AC vuông góc BC
=>AC vuông (SBC)
b: BH vuông góc SC
BH vuông góc AC
=>BH vuông góc (SAC)
=>BH vuông góc SA
c: (SA;ABC)=(AS;SB)=góc ASB
\(BA=\sqrt{CB^2+CA^2}=a\sqrt{3}\)
\(SA=\sqrt{SB^2+BA^2}=a\sqrt{7}\)
sin ASB=AB/SA=căn 3/căn 7
=>góc ASB=41 độ
(SA;(SBC))=(SA;SC)=góc ASC
\(SC=\sqrt{\left(2a\right)^2+a^2}=a\sqrt{5}\)
Vì SC^2+CA^2=SA^2
nên ΔSAC vuông tại C
=>sin ASC=AC/SA=căn 2/căn 7
=>góc ASC=32 độ

Chọn B
Phương pháp
Góc giữa đường thẳng và mặt phẳng (nhỏ hơn 90 o ) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Cách giải:
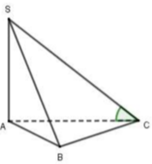
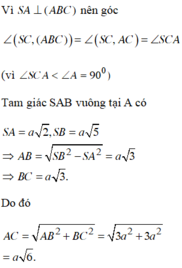
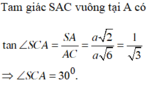

Chọn B.
Phương pháp
Góc giữa đường thẳng và mặt phẳng (nhỏ hơn 90o) là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Cách giải:
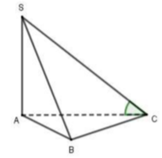


Ta có : \(\left(SBC\right)\cap\left(ABC\right)=BC\)
Lấy H là TĐ của BC \(\Rightarrow AH\perp BC\)
SA \(\perp\left(ABC\right)\Rightarrow SA\perp AB;AC\)
\(\Delta SAB;\Delta SAC\perp\) tại A có : \(SB=\sqrt{SA^2+AB^2}=\sqrt{SA^2+AC^2}=SC\)
\(\Rightarrow\Delta SBC\) cân tại S . Suy ra : \(SH\perp BC\)
Suy ra : \(\left(\left(SBC\right);\left(ABC\right)\right)=\left(HA;HS\right)=\widehat{SHA}\)
Tính được : AH = \(\dfrac{a\sqrt{3}}{2}\)
\(\Delta SAH\) vuông tại A có : \(tan\widehat{SHA}=\dfrac{SA}{HA}=\dfrac{a\sqrt{3}}{2}:\dfrac{a\sqrt{3}}{2}=1\Rightarrow\widehat{SHA}=45^o\)
Vậy ...

Đáp án A
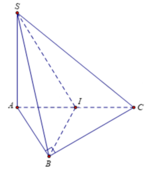
Gọi I là trung điểm của AC. Ta có: A I ⊥ S A C
Khi đó S B ; S A C = B S I ⏜
Đặt S A = A B = B C = a . . Ta có B I = a 2 2 ; S B = a 2
sin B S I ⏜ = B I S B = a 2 2 a 2 = 1 2 ⇒ B S I ⏜ = 30 °
\(SA\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABC)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=AC\sqrt{2}=a\sqrt{2}\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{\dfrac{3}{2}}\Rightarrow\widehat{SBA}\approx50^046'\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
\(\Rightarrow SC\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSC}\) là góc giữa SB và (SAC)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(BC=AC=a\)
\(sin\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{1}{\sqrt{5}}\Rightarrow\widehat{BSC}\approx26^034'\)
b.
Theo cmt, \(BC\perp\left(SAC\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\SA\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow\left(SAC\right)\perp\left(ABC\right)\)
\(\Rightarrow\) Góc giữa (SAC) và (ABC) là 90 độ