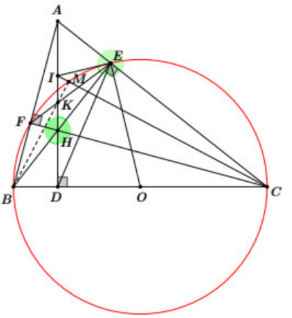
hình ở dưới cùng là hình đúng nha
giải thích giúp mik là sao tam giác ADC lại đồng dạng vs tam giác BDH vậy

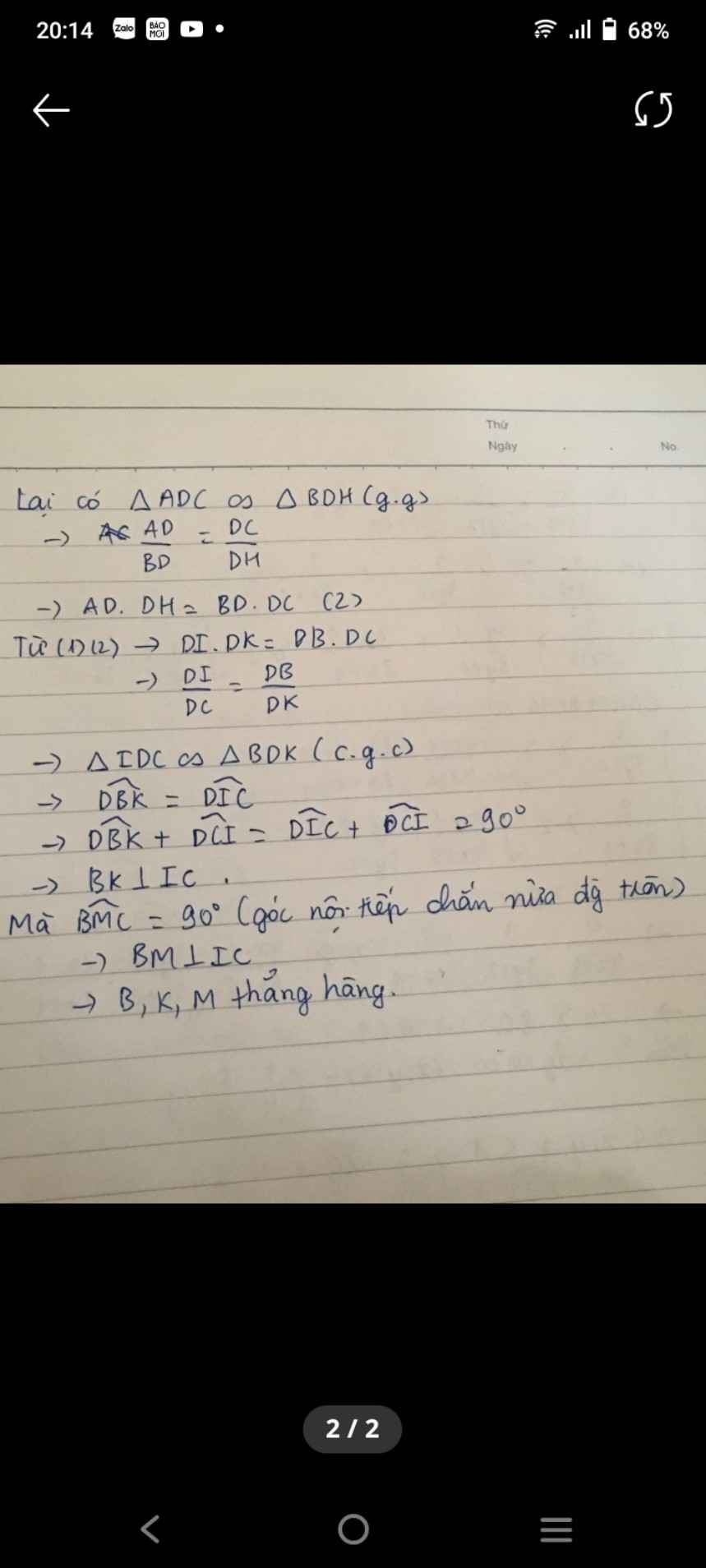
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- △ ABC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
- △ ABC đồng dạng △ HAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ ABC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ∠ (HBA) = ∠ (HAC)
- △ HAB đồng dạng △ NCM
Hai tam giác vuông có góc nhọn ∠ (HAB) = ∠ (NCM)

a) Quan sát hình ta đã thấy diện tích tam giác ADC < diện tích tam giác ABC nhỉ? :)
Nhưng để rõ hơn thì: Có DC = 1/3 BC => DC = 1/2 BD
=> diện tích tam giác ADC = 1/2 diện tích tam giác ABC
b) Vì diện tích tam giác ADC = 1/2 diện tích tam giác ABC
=> DK = 1/2 BH
=> DK = 1/2 x 8,1
=> DK = 4,05 (đơn vị)
Do \(\widehat{ACD}=\widehat{BHD}\) (cùng phụ \(\widehat{DBH}\)) nên 2 tam giác vuông nói trên đồng dạng
Xét tứ giác BADE có :
\(\left\{{}\begin{matrix}\widehat{BDA}=90^o\left(gt\right)\\\widehat{AEB}=90^o\left(gt\right)\end{matrix}\right.\)
mà 2 góc này nằm ở vị trí kề cùng nhìn 1 cạnh
\(\Rightarrow\) TG BADE nội tiếp (O)
Xét \(\Delta ADC\) và \(\Delta BDH\) có :
\(\widehat{ADC}=\widehat{BDH}\left(=90^o\right)\)
\(\widehat{DAC}=\widehat{EBD}\) (cùng chắn \(\stackrel\frown{DE}\) của đtron \(\left(BADE\right)\) )
\(\Rightarrow\Delta ADC\sim\Delta BDH\left(g-g\right)\)