(dm): y = mx - 2m + 1, (P): y= x2 - 3x + 2. Tìm m để d(I;dm) đạt giá trị lớn nhất biết I là đỉnh (P).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 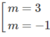
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.

Phương trình hoành độ giao điểm là:
\(x^2-mx+2m-4=0\)
\(\Delta=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16=\left(m-4\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì m-4<>0
hay m<>4
Ta có: \(x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=m^2-2\left(2m-4\right)\)
\(=m^2-4m+8\)
\(=\left(m-2\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi m=2




Tọa độ I là: \(I\left(\dfrac{3}{2};-\dfrac{1}{4}\right)\)
Phương trình \(d_m\): \(m\left(x-2\right)-y+1=0\)
\(\Rightarrow d_m\) luôn đi qua điểm cố định \(A\left(2;1\right)\)
Gọi H là hình chiếu vuông góc của I lên \(d_m\) \(\Rightarrow IH=d\left(I;d_m\right)\)
\(\Rightarrow IH\le IA\) (theo định lý đường xiên - đường vuông góc)
\(\Rightarrow IH_{max}=IA\) khi H trùng A hay \(d_m\) nhận \(\overrightarrow{IA}=\left(\dfrac{1}{2};\dfrac{5}{4}\right)=\dfrac{1}{4}\left(2;5\right)\) là 1 vtpt
\(\Rightarrow\dfrac{m}{2}=\dfrac{-1}{5}\Rightarrow m=-\dfrac{2}{5}\)
Thầy ơi con đang làm theo hướng này thì giải tiếp như thế nào vậy ạ?