Cm : HM song song BC mik nghĩ ko ai lm đc đâu:))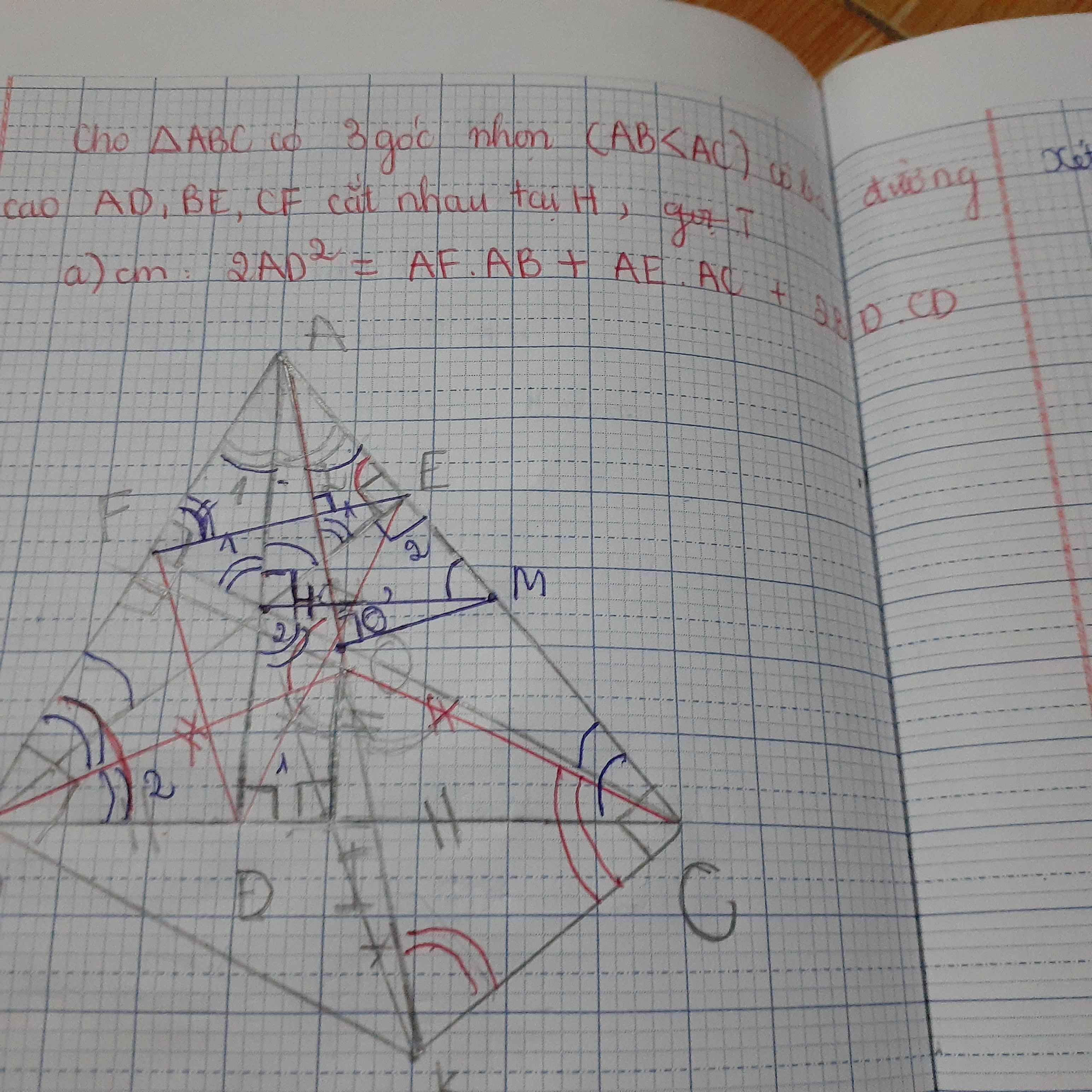
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MD
0
Những câu hỏi liên quan
KT
29 tháng 3 2018
a) Xét \(\Delta HAC\)và \(\Delta MAH\) có:
\(\widehat{AHC}=\widehat{AMH}=90^0\)
\(\widehat{HAC}\) CHUNG
suy ra: \(\Delta HAC~\Delta MAH\)
\(\Rightarrow\)\(\frac{AH}{AM}=\frac{AC}{AH}\)
\(\Rightarrow\)\(AH^2=AM.AC\)
b) \(\Delta AHB~\Delta CHA\)(bn đọc tự chứng minh)
\(\Rightarrow\)\(\frac{AH}{CH}=\frac{HB}{HA}\)
\(\Rightarrow\)\(AH^2=HB.CH\)
mà \(AH^2=AM.AC\)
\(\Rightarrow\)\(AM.AC=HB.CH\)
CM
21 tháng 3 2019
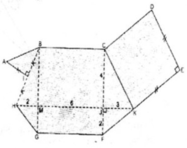
Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB
Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)
⇒ BC = GF = MJ = 6 (cm)
CJ = CF – FG = 6 – 2 = 4 (cm)
S K F G H = (HK + GF)/2. FJ = (11 + 6)/2.2 = 17 ( c m 2 )
S B C K H = (BC + KH)/2. FJ = (11 + 6)/2.4 = 34 ( c m 2 )
Trong tam giác vuông BMH có ∠ J = 90 0 .Theo định lý Pi-ta-go ta có:
C K 2 = C J 2 + J K 2 = 16 + 9 = 25 ⇒ CK = 5 (cm)
S C D E K = C K 2 = 5 2 = 25 ( c m 2 )
Trong tam giác vuông BMH có ∠ M = 90 0 .Theo định lý Pi-ta-go ta có:
B H 2 = B M 2 + H M 2
mà BM = CJ = 4(cm) (đường cao hình thang BCKH)
⇒ B H 2 = 4 2 + 2 2 = 20
IB = BH/2 ⇒ I B 2 = B H 2 / 2 = 20/4 = 5
IB = 5 (cm)
∆ AIB vuông cân tại I (vì AI = IH = IB)
S A I B = 1/2 AI. IB = 1/2 I B 2 = 5/2 ( c m 2 )
S = S C D E K + S K F G H + S B C K H + S A I B = 25 + 17 + 34 + 5/2 = 157/2 ( c m 2 )
LH
31 tháng 7 2017
De et
Dien h tam giac ABC la
40 x 50 : 2 = 1000 ( cm2 )
Dien h hinh AEC la
10 x 50 : 2 = 250 ( cm2 )
Dien h hinh tam giac ABE la
1000 - 250 = 750 ( cm2 )
Doan DE dai la
750 : 40 x 2 = 37,5 ( cm2 )
Chieu cao tam giac BDE la
40 - 10 = 30 ( cm2 )
Dien h tam giac BDE la
37,5 x 30 : 2 = 562,5 ( cm2 )
31 tháng 7 2017
Diện tích hình tam giác ABC là:
40 x 50 : 2 = 1000 ( cm2 )
Diện tích hình AEC là:
10 x 50 : 2 = 250 ( cm2 )
Diện tích hình tam giác ABE là:
1000 - 250 = 750 ( cm2 )
Đoạn DE dài là:
750 : 40 x 2 = 37,5 ( cm2 )
Chiều cao hình tam giác BDE là:
40 - 10 = 30 ( cm2 )
Diện tích tam giác BDE là:
37,5 x 30 : 2 = 562,5 ( cm2 )
Đáp số: 562,5 cm2