Cho tam giác ABC, lấy D trên cạnh BC sao cho CD=1/4BC. Trên tia AD lấy E sao cho D là trung điểm AE. Gọi N là trung điểm BC. CM N là trọng tâm tam giác ABE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


MA=MB; NB=NC => MN là đường trung bình của tg ABC => MN//AC (1)
Xét tg ACD và tg END có
^ADC = ^EDN (góc đối đỉnh)
CN=BC/2; CD=BC/4 => CD=CN/2 hay DC=DN
DA=DE
=> tg ACD = tg END (c.g.c) => ^DAC = ^DEN => EN//AC (2)
Từ (1) và (2) => MN trùng EN (Từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 dt // với đường thẳng đã cho)
=> M;N;E thẳng hàng
CẬU ƠI LỚP 7 ĐÃ HỌC ĐƯỜNG TRUNG BÌNH đâu , bài này tớ có cách khác
A) NỐI B VÀ E
TA CÓ
\(DC=\frac{1}{4}BC\left(1\right)\)
MÀ \(NC=\frac{1}{2}BC\)
THAY \(ND+DC=\frac{1}{2}BC\)
THAY (1) VÀO TA CÓ
\(ND+\frac{1}{4}BC=\frac{1}{2}BC\)
\(\Leftrightarrow ND=\frac{1}{2}BC-\frac{1}{4}BC\)
\(\Leftrightarrow ND=BC\left(\frac{1}{2}-\frac{1}{4}\right)\)
\(\Leftrightarrow ND=\frac{1}{4}BC\)
MÀ \(DC=\frac{1}{4}BC\)
\(\Rightarrow ND=DC\left(2\right)\)
TA LẠI CÓ \(BN=NC\left(gt\right)\)
THAY \(BN=ND+DC\)
THAY (2) VÀO TA CÓ
\(BN=2ND\)
MÀ \(BN+ND=BD\)
THAY \(2ND+ND=BD\)
\(\Leftrightarrow3ND=BD\)
\(\Leftrightarrow ND=\frac{1}{3}BD\)
VÌ AD = DE => BD LÀ ĐƯỜNG TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABE\)
MÀ \(ND=\frac{1}{3}BD\)
=> N LÀ TRỌNG TÂM CỦA \(\Delta ABE\)
VÌ AM=BM
=> EM LÀ ĐƯỜNG TRUNG TUYẾN THỨ 2 CỦA \(\Delta ABE\)
MÀ N LÀ TRỌNG TÂM CỦA \(\Delta ABE\)
=> EM BẮT BUỘT ĐI QUA N
=> BA ĐIỂM E,M,N THẲNG HÀNG (ĐPCM)

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
=>\(\widehat{DAM}=\widehat{EAM}\)
Xét ΔDAM và ΔEAM có
DA=EA
\(\widehat{DAM}=\widehat{EAM}\)
AM chung
Do đó: ΔDAM=ΔEAM
=>MD=ME
c: Xét ΔNKD và ΔNMB có
NK=NM
\(\widehat{KND}=\widehat{MNB}\)(hai góc đối đỉnh)
ND=NB
Do đó: ΔNKD=ΔNMB
=>\(\widehat{NKD}=\widehat{NMB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên KD//BM
mà M\(\in\)BC
nên KD//BC
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Ta có: KD//BC
DE//BC
KD,DE có điểm chung là D
Do đó: K,D,E thẳng hàng

a: Xét ΔABC và ΔAED có
AB=AE
\(\widehat{BAC}=\widehat{EAD}\)
AC=AD
Do đó: ΔABC=ΔAED

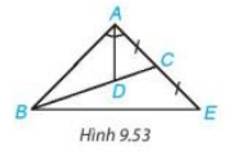
C là trung điểm của AE
\( \Rightarrow \) BC là trung tuyến của tam giác ABE (1)
D thuộc BC, \(BD = 2DC \Rightarrow BD = 2\left( {BC - BD} \right) \Rightarrow 3BD = 2BC \Rightarrow BD = \dfrac{2}{3}BC\)(2)
Từ (1) và (2) suy ra: D là trọng tâm của tam giác ABE
\( \Rightarrow \) AD là đường trung tuyến ứng với BE
Mà AD là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) Tam giác ABE cân tại A.