1 lò xo cố định treo 1 vật có khối lượng m. tần số f=4,5Hz, trong quá trình dao động, l thỏa mãn 40cm<= l <=56cm. gốc tọa độ ở VTCB, chiều dương hướng xuống, gốc thời gian là lúc lò xo ngắn nhất. phương trình dao động là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 6 2016
\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.
VT
14 tháng 1 2017
Đáp án D
A = l max − l min 2 = 56 − 40 2 = 8 ( c m ) ; ω = 2 π f = 10 π t l cân bằng = 56 − 8 = 48 ( c m )
Tại t = 0 ⇒ x = − 4 v < 0 ⇒ cos φ = − 1 2 sin φ > 0 ⇒ φ = 2 π 3
Vậy x = 8 cos 10 π t + 2 π 3
VT
7 tháng 12 2017
Chọn đáp án D
A = l max − l min 2 = 56 − 40 2 = 8 ( c m ) ; ω = 2 π f = 10 π t
l C B = 56 − 8 = 48 ( c m )
Tại t = 0 ⇒ x = − 4 v < 0 ⇒ cos ϕ = − 1 2 sin ϕ > 0 ⇒ ϕ = 2 π 3
Vậy: x = 8 cos 10 π t + 2 π 3
VT
23 tháng 2 2017
Chọn đáp án A.
+ Độ biến dạng của lò xo tại vị trí cân bằng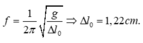 
Biên độ dao động của vật 
+ Chiều dài tự nhiên của lò xo 
VT
10 tháng 6 2017
+ Tại vị trí lực đàn hồi của lò xo bằng 12 N ta có:
F d h = m g + k x → k x = 12 − 1.10 = 2 = F k v với x chính là biên độ dao động của vật.
+ Mặc khác: k . Δ l = m g = 10 > k A
® Δ l > A
® Lực đàn hồi nhỏ nhất tác dụng lên vật là: F d h min = k Δ l − A = k Δ l − k A = 10 − 2 = 8 N
Đáp án C
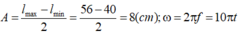
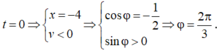
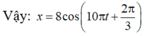
\(f=4,5Hz\Rightarrow\omega=2\pi f=9\pi\) (rad/s)
Biên độ: \(A=\dfrac{l_{max}-l_{min}}{2}=\dfrac{56-40}{2}=8cm\)
Theo bài: (Vẽ hình ta thấy) \(\varphi=-\dfrac{\pi}{2}\)
Vậy pt là \(x=8cos\left(9\pi t-\dfrac{\pi}{2}\right)cm\)