Đoạn thẳng AB có độ dài 28cm. Được chia thành ba đoạn thẳng không bằng nhau theo thứ tự AC, CD và BD. Evaf F là trung điểm của đoạn thẳn AC và BD. Biết độ dài đoạn EF = 16cm. Tìm độ dài đoạn CD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 5 2017
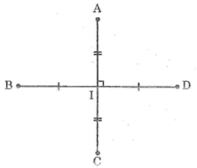
Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm
30 tháng 5 2017
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.
12 tháng 5 2017
Lời giải
a)
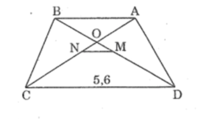
Ta có \(\left\{{}\begin{matrix}MD=MB\\NA=NC\end{matrix}\right.\) \(\Rightarrow\)MN//DC
\(\Rightarrow\Delta OMN\approx\Delta ODC\approx OBA\)
Tỷ số đồng dạng
\(\dfrac{OM}{OD}=\dfrac{MN}{DC}=\dfrac{ON}{OC}\)\(\Rightarrow MN=\dfrac{OM}{OD}.DC=\dfrac{1}{4}.5,6=1,4\left(cm\right)\)
\(\dfrac{OM}{OB}=\dfrac{MN}{AB}\Rightarrow AB=\dfrac{OB}{OM}.MN=2MN=2,8\left(cm\right)\)
b)
\(\left\{{}\begin{matrix}CD=4MN\\AB=2MN\end{matrix}\right.\)
\(\Rightarrow\dfrac{CD-AB}{2}=\dfrac{4MN-2MN}{2}=MN\)
TM
23 tháng 9 2017
vì c là trung điểm => ac = bc = 5cm . cd = 1 => DB = 4 => DE =2 ( vì e là trung điểm ) AE = 8 ( vì ac = 5 và cd = 1 + 2 de ) => F = 5
=> EF = 5 + 2 = 7
23 tháng 9 2017
*Tính CB và CA:
Vì C là trung điểm của AB => CB=CA=AB:2=10:2=5
Vậy CB=5cm; CA=5cm
*Tính BD
=>BD+CD=CB
=>BD+1=5
=>BD=5-1=4
VẬy BD=4cm
*Tính DE, EB:
Vì E là trung điểm của DB
=>DE=EB=BD:2=4:2=2
vậy ĐỀ=2cm; EB=2cm
*TÍnh AE:
=>AE+EB=AB
=>AE+2=10
=>AE=10-2=8
Vậy AE=8cm
*Tính EF:
VÌ F là trung điểm của AE
=>EF=AE:2=8:2=4
vậy EF=4cm
CM
2 tháng 1 2018
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: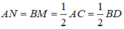 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: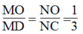 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: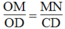 
Hệ quả định lí Ta-lét)
Suy ra: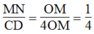 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
24 tháng 1 2015
+, Ta có: AC=AI+IC Mà I lại là trung điểm của AC nên ta có: AC/2=12/2=6(cm) => IA=IC=6(cm) +, Ta có: BD=DI+BI 16=DI+BI Mà I là trung điểm của AC nên ta có: BD/2=16/2=8(cm) +, Ta tam giác AID vuông tại I : =>AD 2 =AI2+ ID2(định lí Pi-Ta-Go) => AD2=62+ 82 => AD2=100 => AD=\(\sqrt{100}\) => AD=10(cm) +, Ta có tam giác AIB vuông tại I => AB 2=AI2+IB2(định lí Pi- Ta- Go) => AB2=62+82 =>AB2= 1OO =>AB=\(\sqrt{100}\) => AB=1O(cm)
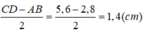
\(E\) là trung điểm của \(AC\) nên \(AE=\)\(\dfrac{AC}{2}\)(1)
\(F\) là trung điểm của \(DB\) nên \(FB=\)\(\dfrac{DB}{2}\)(2)
từ (1) và (2) có:\(AE+FB=\)\(\dfrac{AC}{2}+\dfrac{DB}{2}\Rightarrow AE+FB=\dfrac{AC+BD}{2}\)
Trong đó :\(AE+FB=AB-EF\)
Vậy \(AE +FB=\)\(\dfrac{AC+BD}{2}=28-16=12\)
Suy ra:\(AC+BD=24\)
đoạn \(CD=AB-(AC+BD)=28-24=4cm\)