giải bài toán sau bằng phương pháp thế
a+b=257
a=bx4+2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 1 2023
a: =>8x+2y=4 và 8x+3y=5
=>y=1 và 4x=2-1=1
=>x=1/4 và y=1
b: 3x-2y=11 và 4x-5y=3
=>12x-8y=44 và 12x-15y=9
=>7y=35 và 3x-2y=11
=>y=5 và 3x=11+2*y=11+2*5=21
=>x=7 và y=5
c: 5x-4y=3 và 2x+y=4
=>5x-4y=3 và 8x+4y=16
=>13x=19 và 2x+y=4
=>x=19/13 và y=4-2x=4-38/13=52/13-38/13=14/13
d: 3x-y=5 và 5x+2y=28
=>6x-2y=10 và 5x+2y=28
=>11x=38 và 3x-y=5
=>x=38/11 và y=3x-5=104/11-5=104/11-55/11=49/11
DA
30 tháng 6
a: =>8x+2y=4 và 8x+3y=5
=>y=1 và 4x=2-1=1
=>x=1/4 và y=1
b: 3x-2y=11 và 4x-5y=3
=>12x-8y=44 và 12x-15y=9
=>7y=35 và 3x-2y=11
=>y=5 và 3x=11+2*y=11+2*5=21
=>x=7 và y=5
c: 5x-4y=3 và 2x+y=4
=>5x-4y=3 và 8x+4y=16
=>13x=19 và 2x+y=4
=>x=19/13 và y=4-2x=4-38/13=52/13-38/13=14/13
d: 3x-y=5 và 5x+2y=28
=>6x-2y=10 và 5x+2y=28
=>11x=38 và 3x-y=5
=>x=38/11 và y=3x-5=104/11-5=104/11-55/11=49/11
HB
1
14 tháng 1 2022
a: \(\Leftrightarrow\left\{{}\begin{matrix}5x+25y=45\\-5x-3y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}22y=72\\x+5y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{36}{11}\\x=-\dfrac{81}{11}\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}8x+5y=32\\8x-12y=38\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-6\\4x-6y=19\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{7}{17}\\x=\dfrac{281}{68}\end{matrix}\right.\)
5 tháng 3 2021
Bài 1:
Ta có: \(\left\{{}\begin{matrix}17x+4y=2\\13x+2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}17x+4y=2\\26x+4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-9x=0\\13x+2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(0;\dfrac{1}{2}\right)\)
5 tháng 3 2021
Bài 2:
Gọi x(km/h) là vận tốc của người thứ nhất(Điều kiện: x>0)
Vận tốc của người thứ hai là: x(km/h)
Quãng đường người thứ nhất đi từ A đến chỗ gặp là: 2x(km)
Quãng đường người thứ hai đi từ B đến chỗ gặp là: 2x(km)
Theo đề, ta có: 2x+2x=180
\(\Leftrightarrow4x=180\)
hay x=45(thỏa ĐK)
Vậy: Vận tốc của hai người là 45km/h
19 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
int main()
{
cin>>a>>b>>c>>d;
cout<<min(a,min(b,min(c,d)));
return 0;
}
CM
20 tháng 1 2019
Mặt phẳng (BC’D) có VTPT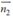 
(1;1; -1) và qua B (1; 0;0) nên có phương trình:
1( x- 1) + 1( y – 0) - 1( z- 0)= 0 hay x + y - z - 1 = 0
Khoảng cách giữa hai mặt phẳng song song (AB’D’) và (BC’D) chính là khoảng cách từ A đến (BC’D) và bằng :
CM
5 tháng 6 2018
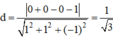
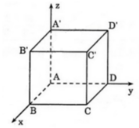
Chọn hệ trục tọa độ Oxyz có gốc O ≡ A;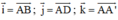 
⇒ A(0; 0; 0) ; B(1; 0; 0); C(1; 1; 0); D(0; 1; 0).
A’(0; 0; 1); B’(1; 0; 1); C’(1; 1; 1); D’(0; 1; 1).
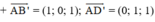
⇒ Vectơ pháp tuyến của (AB’D’) là:
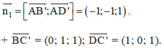
⇒ Vectơ pháp tuyến của (BC’D) là:
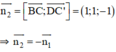
⇒ (AB’D’) // (BC’D).
a+b=257
4xb+2+b=257
4xb+b=257-2
bx(4+1)=255
bx5=255
b=255 : 5
b=51