Cho tam giác ABC vuông tại A trên BC lấy điểm D sao cho BA = BD từ D kẻ đường thẻ vuông góc BC, đường thẻ này cắt AC ở E Từ D kẻ đường thằng song song BE, chứng minh DEC cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


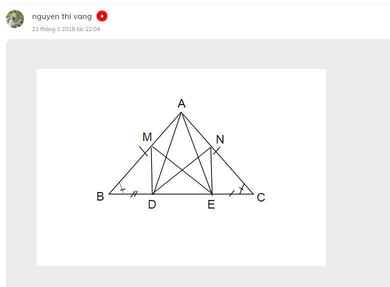
a) Ta có: \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy trong ΔBAC cân tại A)
mà \(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
nên \(\widehat{ABC}=\widehat{ECN}\)
hay \(\widehat{MBD}=\widehat{NCE}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
DB=EC(cmt)
\(\widehat{MBD}=\widehat{NCE}\)(cmt)
Do đó: ΔMBD=ΔNCE(cạnh góc vuông-góc nhọn kề)
Suy ra: DM=EN(hai cạnh tương ứng)

a: Xét ΔBDM vuông tại D và ΔCEN vuông tại E có
BM=CN
góc DBM=góc ECN=góc ACB
=>ΔBDM=ΔCEN
=>MD=EN
b: Xét tứ giác MDNE có
MD//EN
MD=EN
=>MDNE là hình bình hành
=>MN cắt DE tại trung điểm của mỗi đường
=>I la trung điểm của DE
c: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
=>ΔABO=ΔACO
=>BO=CO
mà AB=AC
nên AO là trung trực của BC

Đề sai rồi bạn