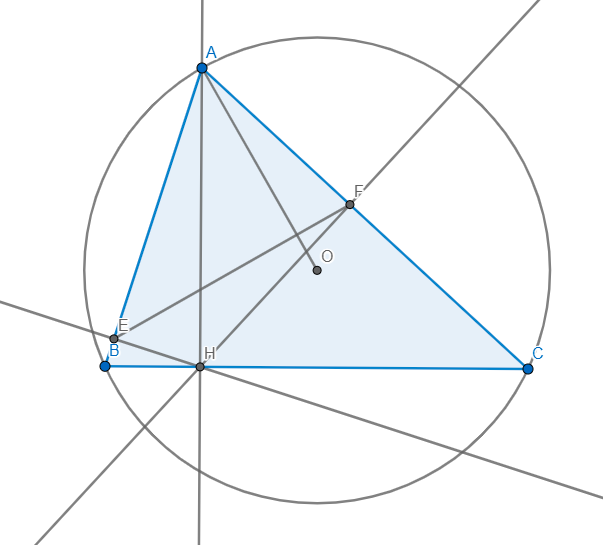
cho tam giác ABC nhọn có đường cao AH , Kẻ He vuông góc với AB ; kẻ HF vuông góc với AC ; BF cắt HE tại M ; CE cắt HF tại N . Trên BC lấy P và Q sao cho tứ giác FPHN và FQHM nội tiếm . Chứng minh rằng PN = QM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 3 2022
Xét tam giác AEH và tam giác AHB, có:
\(\widehat{AHB}=\widehat{AEH}=90^0\)
\(\widehat{A}:chung\)
Vậy tam giác AEH đồng dạng tam giác AHB ( g.g )
AT
16 tháng 7 2021
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)
CM
4 tháng 1 2019
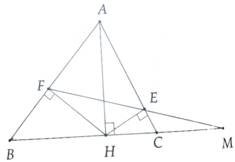
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
11 tháng 4 2023
a: Xét ΔADH vuông tại D và ΔAHB vuông tại H có
góc DAH chung
=>ΔADH đồg dạng vơi ΔAHB
b: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HE là đường cao
nên AE*AC=AH^2
=>AE*AC=AD*AB
27 tháng 4 2018
Ta có: Tứ giác ABDC nội tiếp đường tròn (O) => ^DBC=^CAD (1)
Đường tròn (O) có đường kính AD và điểm B thuộc (O) => ^ABD vuông tại B => AB \(\perp\)BD
=> HE // BD (Quan hệ song song vuông góc) => ^DBC=^BHE (So le trong)
^BHE=^BAH (Cùng phụ ^AHE) => ^DBC=^BAH=^EAH.
Dễ thấy tứ giác AEHF là tứ giác nội tiếp (Tâm là trung điểm của AH)
=> ^EAH=^EFH. Mà ^EAH=^DBC (cmt) => ^EFH=^DBC (2)
Từ (1) và (2) => ^CAD=^EFH
Lại có: ^EFH+^AFE=900 ; ^CAD+^ADC=900 => ^AFE=^ADC
=> ^CAD+^AFE=900 => AD\(\perp\)EF (đpcm)