Một tờ giấy hình vuông cạnh 10 cm được gấp theo đoạn BE như hình vẽ (E là trung điểm của AD). Tính khoảng cách từ F đến CD.
Help cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
Bước 1. Gấp đôi tờ giấy.
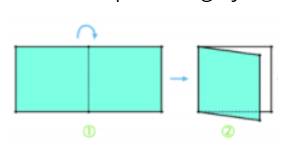
Bước 2: Vẽ một đoạn thẳng nối hai điểm tuỳ ý trên hai cạnh đối diện (cạnh không chứa nếp gấp).
Bước 3: Cắt theo đường vừa vẽ.
Bước 4. Mở tờ giấy ra ta được một hình thang cân.
10 tháng 10 2023
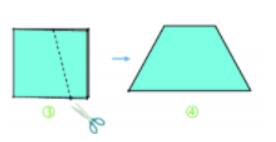
Tham khảo:
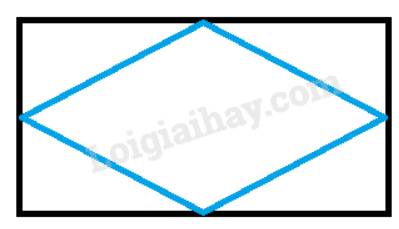
Hình vừa cắt là hình thoi vì có 4 cạnh bằng nhau.
Các đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
27 tháng 12 2021
Bài 2:
b: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
9 tháng 10 2017
1) a) Do ABCD là hình thang cân => góc D = góc C ; góc B = góc A
Trong t/g ABC có : góc A = 90 độ => góc D + góc C2 = 90 độ
Trong t/g ABC có AB = BC ( gt ) => t/g ABC cân tại B => góc A1 = góc C1
Ta có góc A = 90 độ + góc A1 = góc D + góc C2 + góc C1 = góc C + góc C = 2C
Mà :
A + B + C + D = 360 độ = 2A + 2C = 4C + 2C = 6C => góc C = 360 độ : 6 = 60 độ
=> góc C = góc D ( = 60 độ ) ; góc A = góc B ( = 120 độ )