Giải chi tiết giúp mình nha
Vì mình không hiểu mấy bài vậy 😳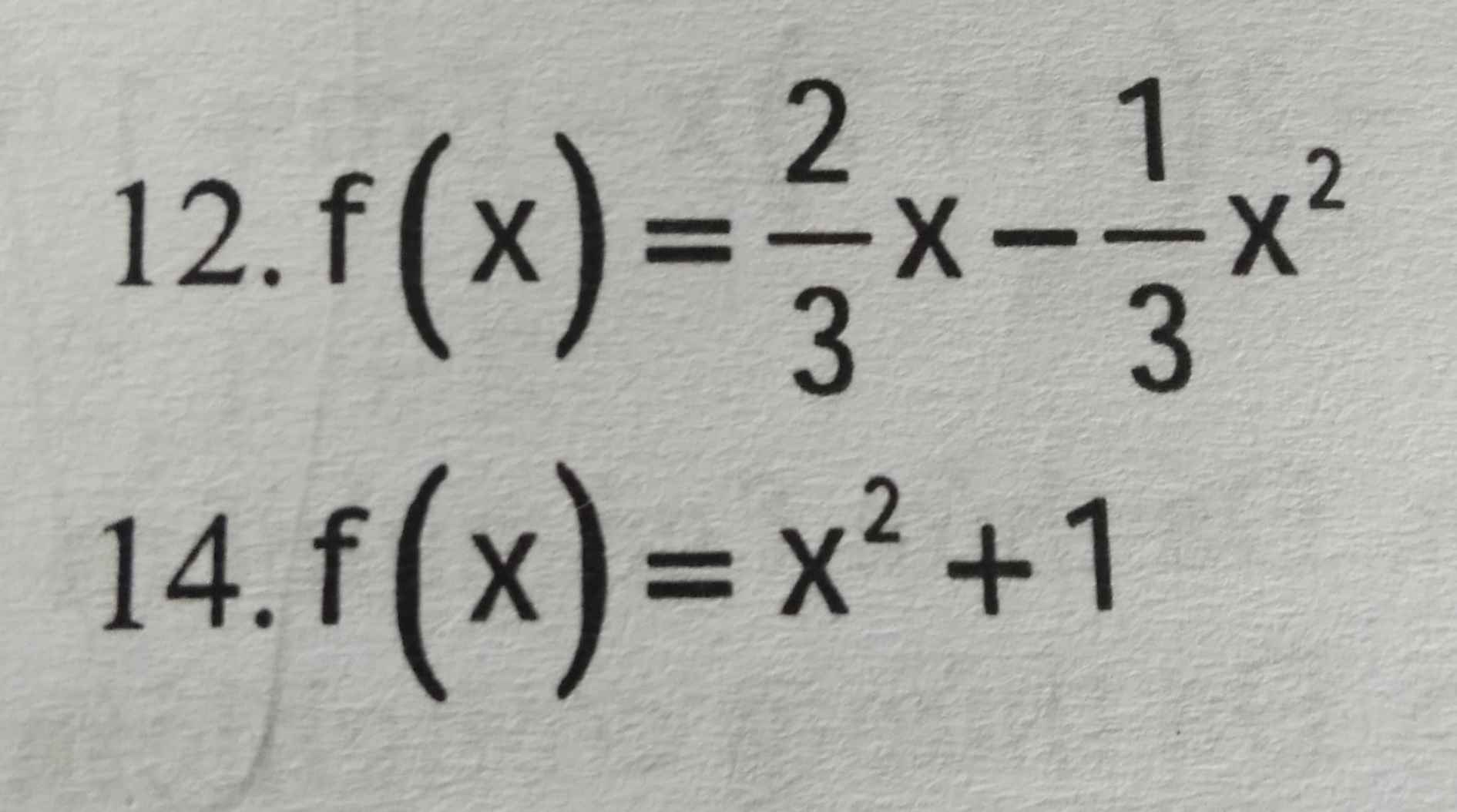
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2021
Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
26 tháng 5 2021
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
AD
5
AT
17 tháng 7 2021
14a) \(M=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}\right)^2+2.\sqrt{2}.2+2^2}-\sqrt{\left(\sqrt{5}\right)^2-2.\sqrt{2}.2+2^2}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
b) \(N=\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{\left(\sqrt{7}\right)^2-2.\sqrt{7}.1+1^2}-\sqrt{\left(\sqrt{7}\right)^2+2.\sqrt{7}.1+1^2}\)
\(=\sqrt{\left(\sqrt{7}-1\right)^2}-\sqrt{\left(\sqrt{7}+1\right)^2}=\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|\)
\(=\sqrt{7}-1-\sqrt{7}-1=-2\)
15a) \(P=\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=\sqrt{3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{3^2-2.3.\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+\sqrt{2}\right)^2}-\sqrt{\left(3-\sqrt{2}\right)^2}=\left|3+\sqrt{2}\right|-\left|3-\sqrt{2}\right|\)
\(=3+\sqrt{2}-3+\sqrt{2}=2\sqrt{2}\)
b) \(Q=\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(=\sqrt{3^2+2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}+\sqrt{3^2-2.3.2\sqrt{2}+\left(2\sqrt{2}\right)^2}\)
\(=\sqrt{\left(3+2\sqrt{2}\right)^2}+\sqrt{\left(3-2\sqrt{2}\right)^2}=\left|3+2\sqrt{2}\right|+\left|3-2\sqrt{2}\right|\)
\(=3+2\sqrt{2}+3-2\sqrt{2}=6\)
15 tháng 9 2021
1: \(100-x^2=\left(10-x\right)\left(10+x\right)\)
2: \(b^2-a^2=\left(b-a\right)\left(b+a\right)\)
3: \(\left(3y\right)^2-\left(4x\right)^2=\left(3y-4x\right)\left(3y+4x\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 8 2021
Đây là 1 lời giải sai em
Đơn giản vì phương trình gốc không thể giải được
ND
1
DT
19 tháng 12 2022
\(CuO+CO\underrightarrow{t^o}Cu+CO_2\)
\(MgO+CO->\left(CO.ko.khử,đc\right)\)
\(Fe_2O_3+3CO\underrightarrow{t^o}2Fe+3CO_2\)
\(FeO+CO\underrightarrow{t^o}Fe+CO_2\)
\(n_{CO_2}=\dfrac{4,48}{22,4}=0,2\left(mol\right)\)
Từ các pthh trên thấy: \(n_{CO_2.sinh.ra}=n_{CO.pứ}=0,2\left(mol\right)\left(theo.tỉ.lệ.pthh\right)\)
Áp dụng ĐLBTKL có: \(m_{hh}+m_{CO}=m_{rắn}+mCO_2\)
=> \(m_{rắn}=m_{hh}+m_{CO}-m_{CO_2}=12,5+0,2.28-0,2.44=9,3\left(g\right)\)
2 tháng 1 2018
A=1+3/2^3+4/2^4+5/2^5+...100/2^100
1/2*A = 1/2 + 3/2^4 + 4/2^5 +....+ 99/2^100 + 100/2^101
A- A/2 = 1/2A =1/2 + 3/2^3 + 1/2^4 +...+1/2^100 - 100/2^101
= [1/2+1/2^2 +1/2^3 +...+1/2^100] -100/2^101 (Do 3/2^3 = 1/2^2 +1/2^3)
=[1-(1/2)^101]/(1-1/2) -100/2^101
=(2^101 -1)/2^100 - 100/2^101
=> A = (2^101 -1)/2^99 - 100/2^100
KH
2 tháng 1 2018
Bạn ơi khó hiểu quá bạn giải chi tiết hơn giúp mình nhé mình sẽ k cho bạn 2 cái nhé
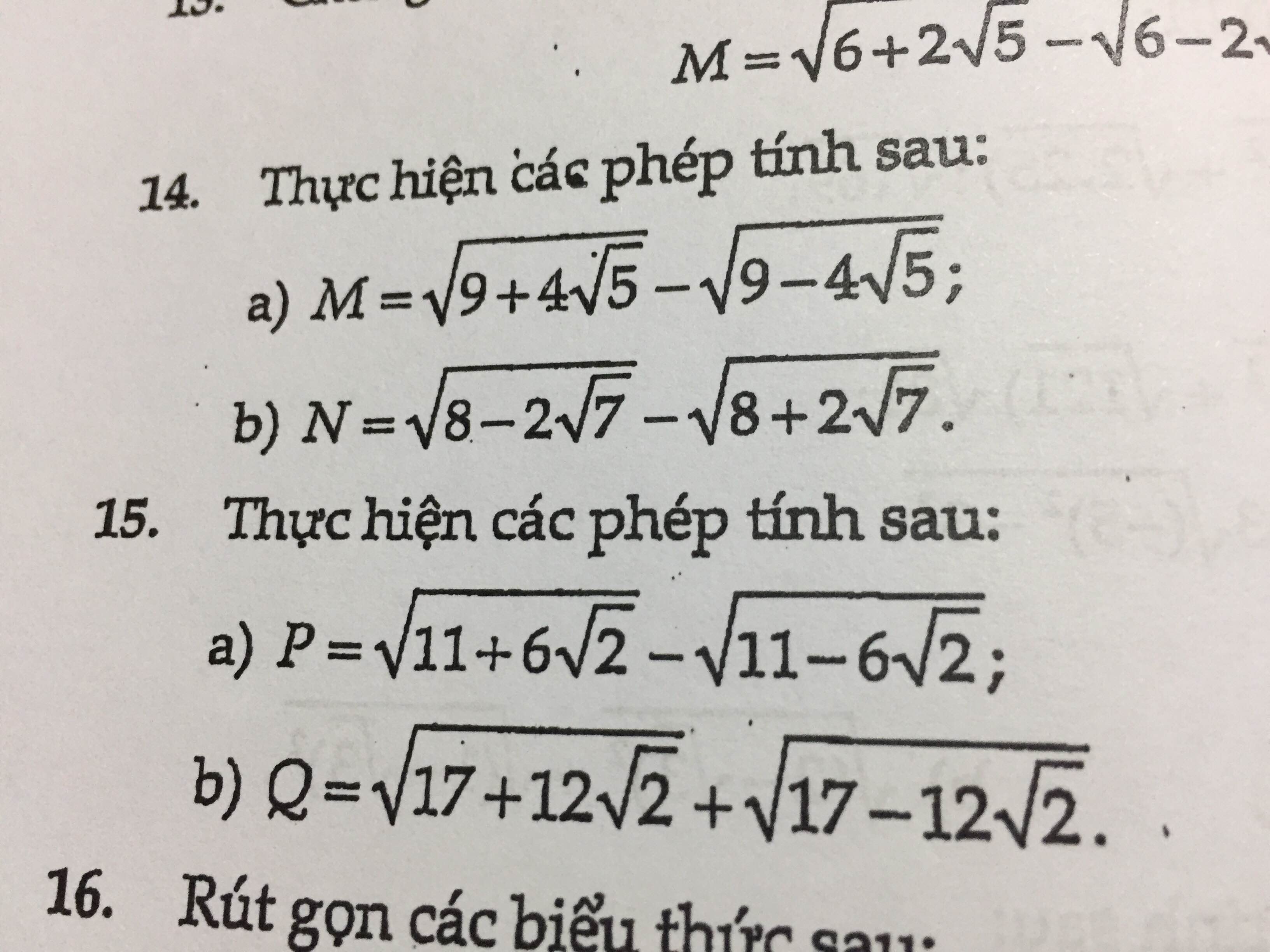
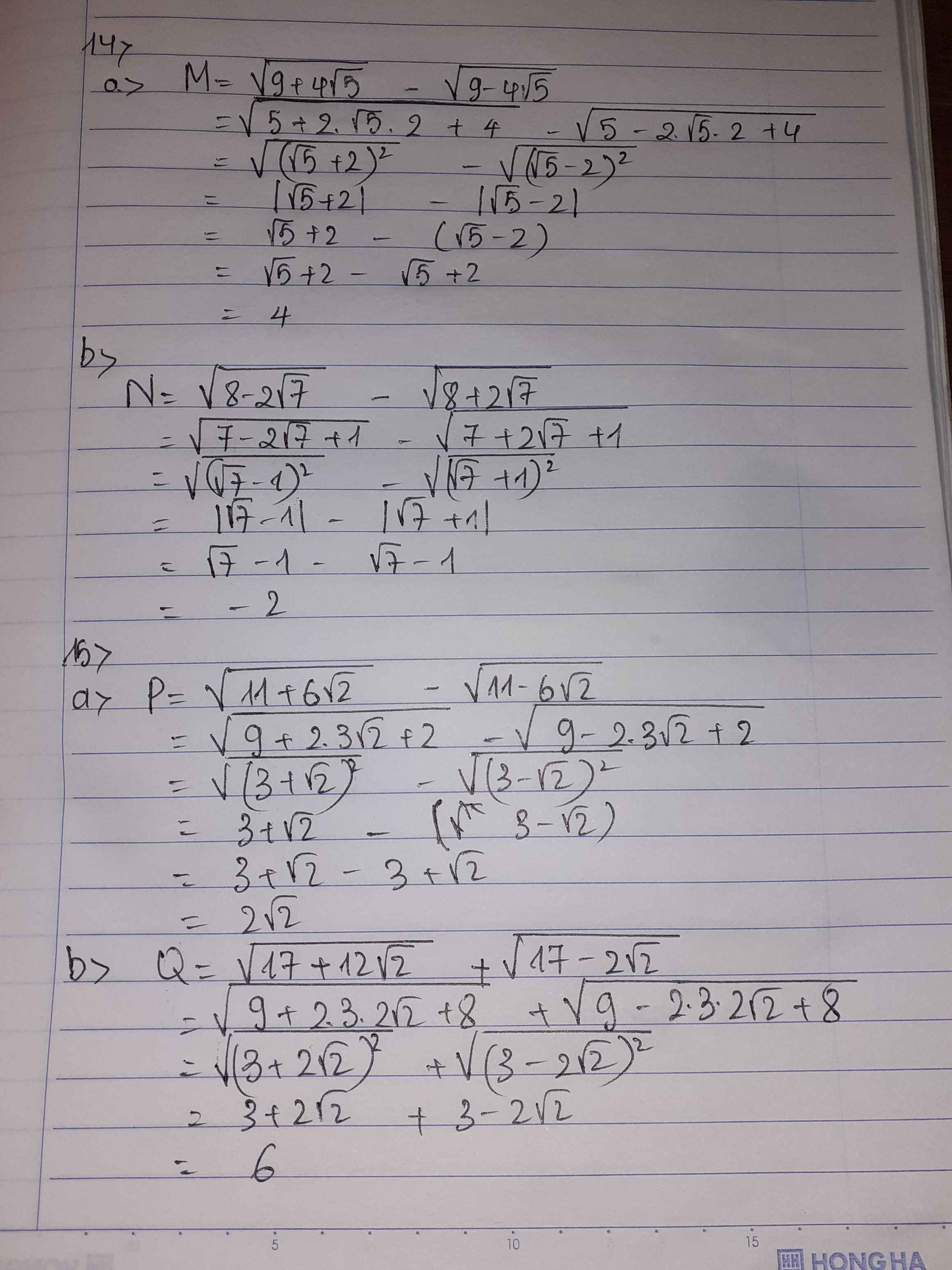
Đề bài yêu cầu gì vậy bạn?
Tìm nghiệm của đa thức