Bài 1
Tính tổng 3 góc ngoài tại 3 đỉnh của 1 tam giác
bài 2
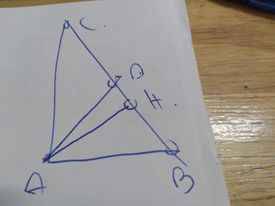
Cho tam giác ABC có góc A=90 , B=60 . Tia phân giác của góc A cắt BC ở D. Kẻ AH vuông góc BC ( H thuộc BC)
a/ tính c
b/ tính ADH
C/ tính HAD
d/ So sánh HAC và ABC
CÁC BẠN VẼ CẢ HÌNH NỮA NHÉ. CẢM ƠN CÁC BẠN


1
Ta đã có định lý góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó và tổng 3 góc trong của một tam giác là 180
Gọi ba góc trong của tam giác là a , b , c . ba góc ngoài tương ứng là a' , b' , c' . Ta có
a+b+c=180
a' = b+c
b' = a+c
c' = a+b
=> a'+b'+c'=b+c+a+c+a+b=2(a+b+c)=2x 180 = 360
Bạn ơi vẽ cả hình nhé