Gieo một đồng xu 3 lần.Xác suất để cả 3 lần gieo đều là mặt ngửa là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
29 tháng 11 2017
xác suất mặt ngửa của đồng A là 1/2,của đồng B là 1/4
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
1.Gieo 2 đồng xu 1 lần,xác suất cả hai đều ngửa là 1/2*1/4 = 1/8
2.2 lần đều ngửa : 1/2*1/4*1/2*1/4 = 1/64
AH
Akai Haruma
Giáo viên
28 tháng 10 2021
Lời giải:
Xác suất để xu 1 ngửa: $\frac{1}{2}$
Xác suất để xu 2 ngửa: $\frac{1}{2}$
Xác suất để xu 3 ngửa: $\frac{1}{2}$
Xác suất để 3 mặt cùng ngửa: $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}=\frac{1}{8}$
CM
24 tháng 4 2018
Chọn A
Ghi nhớ:
-Phép thử “gieo hai đồng tiền phân biệt” thì hai kết quả SN, NS của phép thử là khác nhau.
-Phép thử “gieo n đồng xu phân biệt” thì không gian mẫu có 2 n phần tử, với n ∈ ℕ * .
CM
3 tháng 4 2019
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đo 1 2 n < 1 100 ⇔ n < log 1 2 1 100 ⇒ n ≥ 7 .
Ta cần gieo ít nhất 7 lần
CM
14 tháng 8 2018
Đáp án A
Xác suất để gieo n lần đều mặt ngửa là 1 2 n . Từ đó
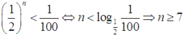
Ta cần gieo ít nhất 7 lần.
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Mỗi lần gieo có 2 khả năng xảy ra: xấp hoặc ngửa
Nếu người đó gieo 3 lần thì có thể có số khả năng xảy ra là:
2.2.2 = 8 (khả năng)
H9
HT.Phong (9A5)
CTVHS
8 tháng 5 2023
Câu 1: Gieo 1 đồng tiền cân đối và đồng chất 2 lần
\(\Rightarrow n\left(\Omega\right)=2^2=4\)
Gọi A là biến cố cả hai lần xuất hiện mặt sấp
\(\Rightarrow A=\left\{SS\right\}\Rightarrow n\left(A\right)=1\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{4}\)
Chọn B
Câu 2: Số phần tử không gian mẫu: \(n\left(\Omega\right)=6\)
Gọi biến cố A: “Số chấm là số nguyên tố xuất hiện”
\(A=\left\{2;3;5\right\}\)
\(\Rightarrow n\left(A\right)=3\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{3}{6}=\dfrac{1}{2}\)
Chọn A
DH
1
16 tháng 4 2023
n(omega)=2*2*2=8
A={(NNS); (NSN); (SNN)}
=>n(A)=3
=>P(A)=3/8
Ta kí hiệu H là mặt ngửa,Q là mặt sấp.Các kết quả có thể là:
QQQ
QQH
QHQ
HQQ
HQH