Cho tam giác ABC cân tại A, đường cao AH=\(a\sqrt{3}\) , BC=3a. BC thuộc (P). Gọi A' là hình chiếu của A lên (P). Tính diện tích tam giác A'BC biết ((P),(ABC))=30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
![]()
Do đó:
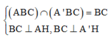
![]()
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
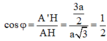
⇒ φ = 60 o

đề có vấn đề đấy bạn, ABC cân A thì AB =AC =12 cm chứ sao AC =16cm đc nhỉ
a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
DO đó: ΔHBA∼ΔABC
b: \(BC=\sqrt{AB^2+AC^2}=20\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\)

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

a: Xet ΔABD vuông tại A và ΔHBI vuông tại H có
góc ABD=góc HBI
=>ΔABD đồng dạng với ΔHBI
b: góc AID=góc BIH=góc ADB=góc ADI
=>ΔADI can tại A

a: \(BC=\sqrt{21^2+28^2}=35\left(cm\right)\)
BD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=35/7=5
=>DB=15cm; DC=20cm
b: AH=21*28/35=16,8cm
c: Xet ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
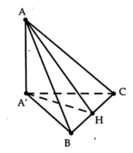

Ta có : A' là h/c của A lên (P) ; BC \(\subset\left(P\right)\) \(\Rightarrow\) \(AA'\perp BC\)
Mà : \(AH\perp BC\) Suy ra : \(BC\perp\left(AA'H\right)\Rightarrow BC\perp A'H\)
Chỉ ra : \(\left(\left(P\right);\left(ABC\right)\right)=\widehat{A'HA}=30^o\)
\(\Delta A'HA\perp\) tại A : \(\dfrac{AH}{A'H}=cos30^o\Rightarrow A'H=\dfrac{\sqrt{3}}{2}.a\sqrt{3}=\dfrac{3a}{2}\)
\(S_{\Delta A'BC}=\dfrac{1}{2}.A'H.BC=\dfrac{1}{2}\dfrac{3a}{2}.3a=\dfrac{9a^2}{4}\)
Sửa lại : \(A'H=2a\)
\(S_{\Delta A'BC}=3a^2\)