nêu đặc điểm của hình vuông và hcn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


HT và HV có 4 cạnh bằng nhau
HV có 4 cạnh bằng nhau còn HCN có 2 cạnh dài bằng nhau và 2 cạnh ngắn bằng nhau
HCN có 4 góc vuông còn HBH có 2 cặp cạnh đối diện song song và bằng nhau
HT có 2 cặp cạnh đối diện song song và bằng nhau còn HV có 4 góc vuông
Nếu đúng bạn tick nha

1. Phương pháp biểu diễn các hình chiếu vuông góc trên cùng một mặt phẳng hình chiếu gọi là phương pháp hình chiếu vuông góc. Có 2 phương pháp chiếu: Phương pháp chiếu góc thứ nhất và phương pháp chiếu góc thứ ba.
2.
- Hình hộp chữ nhật: được bao bởi 2 mặt đáy là hình chữ nhật bằng nhau và 4 mặt bên là các hình chữ nhật.
- Hình lăng trụ tam giác đều: được bao bởi 2 mặt đáy là hình tam giác đều bằng nhau và 3 mặt bên là các hình chữ nhật.
- Hình chóp tứ giác đều: được bao bởi mặt đáy là hình vuông và 4 mặt bên là các hình tam giác đều bằng nhau.
- Hình trụ: có hình chiếu đứng và hình chiếu cạnh là hình chữ nhật; hình chiếu bằng là hình tròn
- Hình nón: có hình chiếu đứng và hình chiếu cạnh là hình tam giác, hình chiếu bằng là hình tròn.
- Hình cầu: cả ba hình chiếu đứng, bằng, cạnh là hình tròn có cùng đường kính.
3.
Đối với khối đa diện đều, cần 3 hình chiếu để đủ biểu diễn hình dạng và kích thước
4.
Các bước vẽ hình chiếu vuông góc của vật thể:
- Bước 1: Phân tích vật thể thành các thể khối đơn giản
- Bước 2: Chọn các hướng chiếu
- Bước 3: Vẽ các hình chiếu các bộ phận của vật thể bằng nét liền mảnh
- Bước 4: Hoàn thiện các nét vẽ và ghi kích thuớc
5.
– Gồm 5 bước:
1. Khung tên.
2. Hình biểu diễn.
3. Kích thước.
4. Yêu cầu kĩ thuật.
5. Tổng hợp.
6.
1. Khung tên
2. Bảng kê
3. Hình biểu diễn
4. Kích thước
5. Phân tích chi tiết
6. Tổng hợp

h vuông và hình chữ nhật có 4 cạnh bằng nhau khác nhau hình chữ nhật cạnh dài cạnh ngắn còn hình vuông 4 cạnh đều bằng nhau
'Ơ;.L, Hình chữ nhật hình bình hành đều có các cặp

Hình thang vuông có hai cạnh đáy song song và vuông góc với hai đáy, tạo nên góc 90 độ.
Hình thang vuông có hai cạnh đáy song song và vuông góc với hai đáy, tạo nên góc 90 độ.

Bốn cạnh bằng nhau
Bốn góc bằng nhau
Hai đường chéo bằng nhau
Hai đường chéo là đường trung trực của nhau
Hai đường chéo là hai đường phân giác của 4 góc trong hình vuông

Đặc điểm hình vuông là có 4 cạnh bằng nhau , có 4 góc vuông
mk nghĩ có như vậy thôi

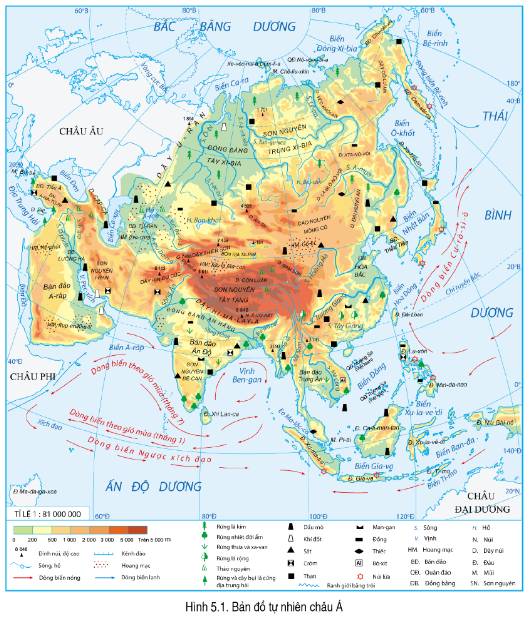
- Đặc điểm địa hình châu Á: phân hóa đa dạng.
+ Núi, cao nguyên và sơn nguyên chiếm ¾ diện tích châu lục, phần lớn tập trung ở khu vực trung tâm. Các dãy núi chạy theo hai hướng chính là bắc – nam và đông – tây.
+ Các đồng bằng châu thổ rộng lớn phân bố chủ yếu ở phía đông và nam.
+ Địa hình ven biển và hải đảo bị chia cắt mạnh tạo thành các vũng, vịnh….
- Đặc điểm khoáng sản châu Á:
+ Tài nguyên khoáng sản đa dạng, phong phú.
+ Một số khoáng sản có trữ lượng lớn như: than, dầu mỏ, khí đốt, sắt, thiếc, crom, man-gan,…
- Ý nghĩa của đặc điểm địa hình và khoáng sản đối với việc sử dụng và bảo vệ tự nhiên ở châu Á:
+ Tạo điều kiện cho châu Á phát triển nhiều ngành kinh tế.
+ Cần hạn chế các tác động tiêu cực làm biến đổi địa hình, ô nhiễm môi trường,...

a: Xét tứ giác AIKD có
AI//KD
AI=KD
AI=AD
=>AIKD là hình thoi
mà góc A=90 độ
nên AIKD là hình vuông
Xét tứ giác BIKC có
BI//KC
BI=KC
BI=BC
=>BIKC là hình thoi
mà góc B=90 độ
nên BIKC là hình vuông
b: Xét ΔDIC có
IK vừa là đường cao, vừa là trung tuyến
IK=1/2DC
Do đó: ΔDIC vuông cân tại I
c: AIKD là hình vuông
=>AK vuông góc ID tại trung điểm của mỗi đường và AK=ID
=>AK=ID và AK vuông góc ID tại S
=>SI=SK
BIKC là hình vuông
=>CI vuông góc BK tại trung điểm của mỗi đường và CI=BK
=>CI vuông góc BK tại R
=>RI=RC=RK=RB
Xét tứ giác ISKR có
góc ISK=góc IRK=góc SIK=90 độ
Do đó: ISKR là hình chữ nhật
mà SI=SK
nên ISKR là hình vuông
Hình vuông có đặc điểm là có hai cạnh song song, có 4 cạnh bằng nhau, có 4 góc vuông
Hình chữ nhật có hai cạnh song song và có 4 goc vuông
hình vuông:
Trong hình học Euclid, hình vuông là một hình tứ giác đều. Có thể coi hình vuông là một hình chữ nhật có các cạnh bằng nhau, hoặc là một hình thoi có hai đường chéo bằng nhau.
Tọa độ đề các của các đỉnh của một hình vuông có tâm ở gốc hệ tọa độ và mỗi cạnh dài 2 đơn vị, song song với các trục tọa độ là (±1, ±1). Phần trong của hình vuông đó bao gồm tất cả các điểm (x0, x1) với -1 < xi < 1.
hình chữ nhật:
Hình chữ nhật trong hình học Euclid là một hình tứ giác có ba góc vuông[1]. Từ định nghĩa này, ta thấy hình chữ nhật là một tứ giác lồi có bốn góc vuông[1]. Đây làhình bình hành có hai đường chéo bằng nhau.