Em cần một bài giải mẫu cho dạng bài này ạ. Em cảm ơn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BDO+góc OMB=90+90=180 độ
=>BDOM nội tiếp
góc BCE=góc CAE
góc DOM+góc MBD=180 độ
góc MBD=góc NAE
=>góc DOM+góc NAE=180 độ
b: OD vuông góc BE
=>D là trung điểm của BE
ΔBEC có MD là đường trung bình
=>MD//EC
=>DF//CE
DF//CE
=>ΔNFD đồng dạng với ΔNCE
=>NF/NC=ND/NE
=>NF*NE=NC*ND

a: Phương trình hoành độ giao điểm là:
\(-x^2-2mx+m^2-4=0\)
\(\text{Δ}=\left(-2m\right)^2-4\cdot\left(-1\right)\cdot\left(m^2-4\right)=4m^2+4\left(m^2-4\right)=4m^2+4m^2-16=8m^2-16\)
=>Đề sai rồi bạn

vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )

Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)
\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)
\(x^3=14-3x\)
\(x^3+3x-14=0\)
\(\left(x-2\right)\left(x^2+2x+7\right)=0\)
\(x=2\)
\(\Rightarrow\dfrac{m}{n}=2\)
\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên

a: Khi x=2 thì (1) sẽ là:
4-2(m+2)+m+1=0
=>m+5-2m-4=0
=>1-m=0
=>m=1
x1+x2=m+1=3
=>x2=3-2=1
b: Δ=(m+2)^2-4(m+1)
=m^2+4m+4-4m-4=m^2>=0
=>Phương trình luôn có hai nghiệm
P=(x1+x2)^2-4x1x1+3x1x2
=(x1+x2)^2-x1x2
=(m+2)^2-m-1
=m^2+4m+4-m-1
=m^2+3m+3
=(m+3/2)^2+3/4>=3/4
Dấu = xảy ra khi m=-3/2

\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)




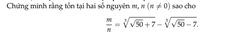



Tọa độ giao điểm của (d2) và (d3) là:
\(\left\{{}\begin{matrix}2x-3y=5\\x+2y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Vì (d) song song với (d1) nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=-1 vào (d), ta được:
b+2=-1
hay b=-3
Em cảm ơn ạ.