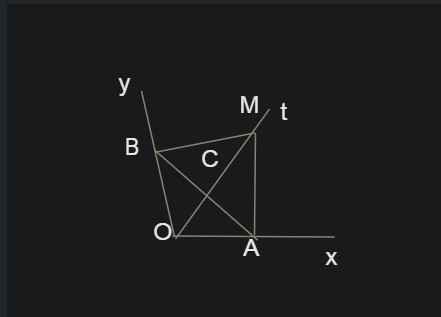
Cho góc xOy nhọn, phân giác Ot. Trên Ot lấy M. Vẽ A đối xứng M qua Ox ; B đối xứng M qua Oy . Chứng minh À đối xứng B qua OM.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>MA=MB và OA=OB
b: M đối xứng D qua Ox
=>OM=OD
M đối xứng E qua Oy
=>OE=OM
=>OD=OE

a) Xét t/g AOM và t/g BOM có:
OA = OB (gt)
AOM = BOM (gt)
OM là cạnh chung
Do đó, t/g AOM = t/g BOM (c.g.c) (đpcm)
b) t/g AOM = t/g BOM (câu a)
=> OA = OB (2 cạnh tương ứng) (đpcm)
c) t/g AOM = t/g BOM (câu a)
=> OAM = OBM (2 góc tương ứng) (1)
Lại có: AB // CD (gt)
=> OAM = OCH ( đồng vị) (2)
OBM = ODH ( đồng vị) (3)
Từ (1); (2) và (3) => OCH = ODH
Dựa vào tổng 3 góc của tam giác dễ dàng => CHO = DHO
Mà CHO + DHO = 180o ( kề bù)
=> CHO = DHO = 90o
=> OH _|_ CD ( đpcm)

a) Xét tam giác vuông AMO và tam giác vuông BMO :
góc MOA = góc MOB (gt)
OM là cạnh chung
=>tam giác vuông AMO = tam giác vuông BMO (cạnh huyền + góc nhọn)
=> OA=OB ( 2 cạnh tương ứng)
b) theo a) ta có : tam giác AMO = tam giác BMO
=>góc AMO = góc BMO
=> MO là tia phân giác của góc AMB
c) gọi C là giao điểm của OM và AB
Xét tam giác OAC và tam giác OBC có:
góc AOC = góc BOC (gt)
OC là cạnh chung
OA = OB (theo a)
=>tam giác OAC = tam giác OBC
=> góc ACO = góc BCO
mà hai góc này kề bù
=> góc ACO = góc BCO = 90 độ
=> OM vuông góc với AB
a, ΔOIN=ΔOIP(g.c.g)⇒IN=IPΔOIN=ΔOIP(g.c.g)⇒IN=IP ( 2 cạnh tương ứng)
Mà Ot⊥NPOt⊥NPnên N và P đối xứng với nhau qua trục Ot.
b, Xét tứ giác ONMP có: I là trung điểm của NP (gt)
I là trung điểm của OM (gt)
⇒ONMP⇒ONMPlà hình bình hành.
Mà 2 đường chéo OM và NP vuông góc với nhau
⇒ONMP⇒ONMPlà hình thoi.
c, ˆxOy=900⇒ONMPxOy^=900⇒ONMP là hình vuông.
Chúc bạn học tốt.