trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(4;3), B(2-1) và C(-4;1)a)Viết phương trình đương cao AH của tam giác ABC b)VIết phương trình đường thẳng d, biết d đi qua điểm A và cắt tia Ox,Oy thứ tự tại M và N sao cho tam giác OMN có diện tích nhỏ...
Đọc tiếp
trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(4;3), B(2-1) và C(-4;1)
a)Viết phương trình đương cao AH của tam giác ABC
b)VIết phương trình đường thẳng d, biết d đi qua điểm A và cắt tia Ox,Oy thứ tự tại M và N sao cho tam giác OMN có diện tích nhỏ nhất
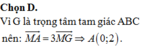
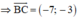
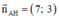là VTPT là:
\(BC:x+3y+1=0\)
\(\overrightarrow{n_{BC}}=\left(1,3\right)\Rightarrow\overrightarrow{u_{BC}}=\left(-3,1\right)\)
Phương trình đường cao \(AH\)có dạng: \(-3x+y+c=0\)
\(AH\)đi qua \(A\left(4,3\right)\Rightarrow AH:-3x+y+9=0\)
Gọi giao điểm của đường thẳng \(d\)với hai tia \(Ox,Oy\)lần lượt là \(\left(m,0\right),\left(n,0\right)\)(\(m,n>0\))
suy ra \(d:\frac{x}{m}+\frac{y}{n}=1\)
Mà \(d\)đi qua \(A\left(4,3\right)\)nên \(\frac{4}{m}+\frac{3}{n}=1\)
\(S_{OMN}=\frac{mn}{2}\)
Ta cần tìm giá trị nhỏ nhất của \(mn\)với \(\frac{4}{m}+\frac{3}{n}=1\)và \(m,n>0\).
Ta có: \(1=\frac{4}{x}+\frac{3}{y}\ge2\sqrt{\frac{12}{xy}}\Rightarrow xy\ge4.12=48\)
Dấu \(=\)xảy ra khi \(m=8,n=6\).
Vậy \(d:\frac{x}{8}+\frac{y}{6}=1\)là đường thẳng thỏa mãn ycbt.