Cho a = 4, b = 64, c = 2. Tính logab, logca, logcb.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có log c a = log c b . log b a
= 1 log a b . log c = 1 2 . 3 = 1 6
Chọn đáp án D.

Ta có
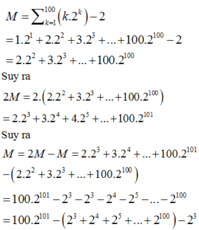
Xét tổng 2 3 + 2 4 + . . + 2 100 là tổng của 98 số hạng của cấp số nhân có u 1 = 2 3 và công bội q = 2 .
Nên
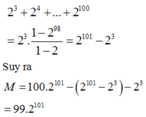
Từ đó
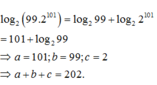
Chọn B.

Xét mệnh đề
log c a + b + log c a - b = 2 ⇔ log c a + b a - b = 2 ⇔ a 2 - b 2 = c
(luôn đúng)
* Xét mệnh đề
log sin x 1 + cos x + log sin x 1 - cos x = 2 ⇔ log sin x 1 - cos 2 x = 2 ⇔ 1 - cos 2 x = sin 2 x
(luôn đúng).
Đáp án D

Nhận thấy các đáp án đều có tích xy nên ta sẽ tính tích này.
Ta có ![]()

Chọn C.

Áp dụng bất đẳng thức Cauchy cho ba số dương
I = log a b + log b c + log c a ≥ 3 log a b . log b c . log c a 3 Đ I I = log a b 2 + log b c 2 + log c a 2 ≥ 3 log a b 2 . log b c 2 . log c a 2 3 S
Đáp án A
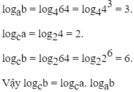
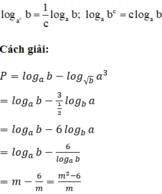

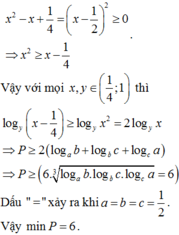
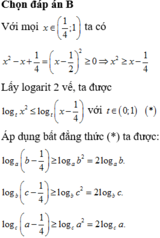
TL :
logab = log464 = log443 = 3
logca = log24 = 2
logcb = log264 = log226 = 6
Vậy logcb = logca. logab
đây mà là lớp 1 á???