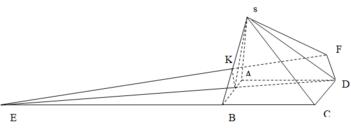
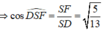Trong hình vẽ bên dưới, ABCD và CGEF là hai hình chữ nhật, trong đó A nằm trên cạnh EG của hinh chữ nhật CGEF và F nằm trên cạnh AB của hình chữ nhật ABCD sao cho thỏa mãn điều kiện FB : AF = 3 : 2. Biết diện tích hình chữ nhật ABCD bằng 5055 cm2 . Tính diện tích hình chữ nhật CGEF. E, ...
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
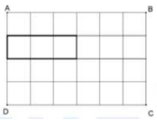
Lưới hình vuông ở trên được tạo thành bởi 7 đường kẻ dọc và 5 đường kẻ ngang. Với mỗi cách chọn hai đường kẻ ngang và hai đường kẻ dọc ta thu được đúng một hình chữ nhật với các đỉnh là giao điểm của các đường đó. Từ đó suy ra số hình chữ nhật cần tìm là:
C 7 2 . C 5 2 = 210 .

\(S_{DEF}=\dfrac{1}{3}\cdot S_{ABCD}=\dfrac{1}{3}\cdot2\cdot S_{ABD}=\dfrac{2}{3}\cdot S_{ABD}\)
\(S_{DFB}=\dfrac{1}{2}\cdot DA\cdot FB=\dfrac{1}{2}\cdot4\cdot5=2\cdot5=10\)
\(S_{DAE}=\dfrac{1}{2}\cdot4\cdot5=2\cdot5=10\left(cm^2\right)\)
=>\(10+10=\dfrac{1}{3}\cdot S_{ABD}=\dfrac{1}{3}\cdot\left(5+5+EF\right)\cdot4=\dfrac{2}{3}\cdot\left(10+FE\right)\)
=>2/3(FE+10)=20
=>FE+10=20:2/3=20*3/2=30
=>FE=20cm

Đáp án B
Kẻ H K ⊥ S B ⇒ H K ⊥ ( S C B ) .
Gọi E = D H ∩ B C , kẻ D F / / H K ( F ∈ E K )
⇒ D F ⊥ ( S B C )
![]()
Ta có S H = S A 2 - A H 2 = 2 a .
Xét ∆ S H B có 1 H K 2 = 1 S H 2 + 1 H B 2 = 13 36 a 2
⇒ H K = 6 a 13
Ta có E H E D = H B C D = 3 4 .
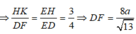
Ta có S D = S H 2 + D H 2 = 2 a 2