cho O là điểm tùy ý trong tam giác abc. biết AM = 1/3 AO, BN= 1/3 BO, CP= 1/3 CO. Tính diện tích tam giác MNP biết diện tích tam giác ABC là 90 cm2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 6 2023
S MON=20cm2
=>S NAM=60cm2
=>S AMC=120cm2
=>S ABC=240cm2
25 tháng 6 2023
Cho tui tick nha
Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC
Diện tích tam giác ABN là:
64 x 1/4 = 16 (cm2 )
Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA
Diện tích tam giác BMN là:
16 x 1/2 = 8 (cm2 )
Đáp số: 8 cm2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 6 2023
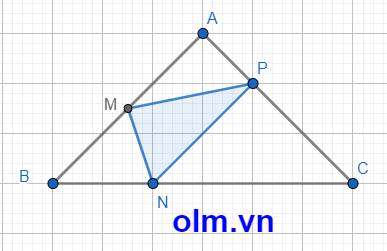
SAMP = \(\dfrac{1}{2}\)SABP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy AB và AM = \(\dfrac{1}{2}\)AB)
AP = AC - PC = AC - \(\dfrac{2}{3}\) AC = \(\dfrac{1}{3}\)AC
SAPB = \(\dfrac{1}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và AP = \(\dfrac{1}{3}\) AC)
⇒ SAMP = \(\dfrac{1}{2}\times\)\(\dfrac{1}{3}\)SABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm2)
SBMN = \(\dfrac{1}{2}\)SABN (vì hai tam giác có chung chiều cao hạ từ đỉnh N xuống đáy AB và BM = \(\dfrac{1}{2}\) AB)
SABN = \(\dfrac{1}{3}\)SABC (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BC và BN = \(\dfrac{1}{3}\)BC)
SBMN = \(\dfrac{1}{2}\times\) \(\dfrac{1}{3}\)SABC = 36 \(\times\) \(\dfrac{1}{6}\) = 6 (cm2)
CN = BC - BN = BC - \(\dfrac{1}{3}\)BC = \(\dfrac{2}{3}\)BC
SCNP = \(\dfrac{2}{3}\)SBCP (vì hai tam giác có chung chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{2}{3}\) BC)
SBCP = \(\dfrac{2}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AC và PC = \(\dfrac{2}{3}\)CA)
SCNP = \(\dfrac{2}{3}\times\dfrac{2}{3}\) = \(\dfrac{4}{9}\)\(\times\)36 = 16 (cm2)
Diện tích tam giác MNP là:
36 - (6+6+16) = 8 (cm2)
Đáp số: 8 cm2
AM=1/3AO
=>OM=2/3AO
BN=1/3BO
=>ON/OB=2/3
CP=1/3CO
=>OP/OC=2/3
Xét ΔOAC có OM/OA=OP/OC
nên MP//AC và MP/AC=OM/MA
=>ΔOMP đồng dạng với ΔOAC
=>S OMP/S OAC=(OM/OA)^2=(2/3)^2=4/9
Xét ΔOAB có OM/OA=ON/OB
nên MN//AB
=>ΔOMN đồng dạng với ΔOAB
=>S OMN/S OAB=(OM/OA)^2=(2/3)^2=4/9
Xét ΔOBC có ON/OB=OP/OC
nên NP//BC
=>ΔONP đồng dạng với ΔOBC
=>S ONP/S OBC=(ON/OB)^2=4/9
=>S MNP=4/9*S ABC=40cm2