1, Cho a/b = b/c = c/a
chứng minh : a = b = c ( 2 cách)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :\(\text{VT = A + B}\)
\(\text{= ( a + b + 5 ) + ( b – c – 9 )}\)
\(\text{= a + b + 5 + b – c – 9}\)
\(\text{= a + ( b + b ) – c + ( 5 – 9 )}\)
\(\text{= a + 2b – c – 4 (1)}\)
\(\text{VP = C – D}\)
\(\text{= ( b – c – 4 ) – ( -b – a )}\)
\(\text{= b – c – 4 + b + a}\)
\(\text{= ( b + b ) – c + a – 4}\)
\(\text{= 2b – c + a – 4}\)
\(\text{= a + 2b – c – 4 (2)}\)
\(\text{từ (1) và (2) suy ra}\)\(\text{ A + B = C – D ( đpcm ) }\)


1. Xét \(\Delta ABC\) vuông tại A có :
BC > AC ( ch > cgv) ; BC > AB .
2 . a) + b) Xét \(\Delta ABE\) và \(\Delta HBE\) có :
\(\widehat{BAC}=\widehat{EHB}=90^o;BE:chung;\widehat{ABE}=\widehat{HBE}\)
\(\Rightarrow\) \(\Delta ABE\) = \(\Delta HBE\) ( ch- gn)
\(\Rightarrow\) AB = HB
\(\Rightarrow\) \(\Delta ABH\) cân tại B mà BE là phân giác \(\Rightarrow\) BE là đường cao
\(\Rightarrow\) \(BE\perp AH\)
3.a) Xét \(\Delta ABC\) vuông tại A
\(\Rightarrow\) \(\widehat{ABC}+\widehat{BCA}=90^o\Rightarrow\widehat{ACB}=30^o\) ( 1 )
Có BE là phân giác \(\Rightarrow\) \(\widehat{ABE}=\widehat{EBC}=\frac{60^o}{2}=30^o\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\Delta EBC\) cân tại E mà EH là đường cao \(\Rightarrow\) EH là trung tuyến hay BH = CH
b) Xét \(\Delta EHC\) vuông tại H
\(\Rightarrow\) \(EC>HC\left(ch>cgv\right)\)
mà AB = BH ; BH = HC \(\Rightarrow\) \(EC>AB\)

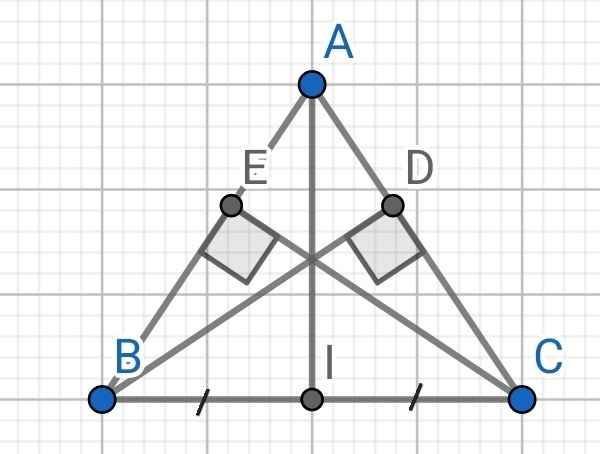 a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC


Ta cần tìm m để BĐT dưới là đúng
\(\frac{1}{a^2+b+c}=\frac{1}{a^2-a+3}\le\frac{1}{3}+m\left(a-1\right)\Leftrightarrow-\frac{a\left(a-1\right)}{3\left(a^2-a+3\right)}\le m\left(a-1\right)\)
Tương tự như trên ta dự đoán rằng\(m=\frac{-1}{9}\)thì BĐT phụ đúng
\(\frac{1}{a^2-a+3}\le\frac{4}{9}-\frac{a}{9}\Leftrightarrow0\le\frac{\left(a-1\right)^2\left(3-a\right)}{3\left(a^2-a+3\right)}\Leftrightarrow0\le\frac{\left(a-1\right)^2\left(b+c\right)}{3\left(a^2-a+3\right)}\)
Cmtt ta được
\(\frac{1}{b^2-b+3}\le\frac{4}{9}-\frac{b}{9};\frac{1}{c^2-c+3}\le\frac{4}{9}-\frac{c}{9}\)
Cộng theo vế của BĐT trên ta được
\(\frac{1}{a^2+b+c}+\frac{1}{b^2+a+c}+\frac{1}{c^2+b+a}\le\frac{4}{3}-\frac{a+b+c}{9}=1\)
=> ĐPCM
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{b+c+a}=1\)=> a = b ; b = c ; c = a => a = b = c
Đặt a/b = b/c = c/a = k thì a = bk ; b = ck ; c = ak
=> a = bk = ck.k = ak.k2 = ak3 => 1 = k3 => k = 1 => a = b ; b = c ; c = a => a = b = c
Cách 1: Áp dụng tính chất của dãy tỉ số ta có:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=\frac{a+b+c}{a+b+c}=1\)
=> a = b = c (đpcm)
Cách 2: Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{a}=k\)
=> \(k^3=\frac{a}{b}.\frac{b}{c}.\frac{c}{a}=1=1^3\)
=> k = 1
=> a = b = c (đpcm)