Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D

Bài 4: a) Xét ABE vàHBE có:
BE chung
ABE= EBH (vì BE là phân giác)
=> ABE=HBE (cạnh huyền- góc nhọn)
b, Vì ABE=HBE(cmt)
=> BA = BH và EA = EH
=> điểm B, E cách đều 2 mút của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c, Vì AC vuông góc BK => EAK = \(90\) độ
EH vuông góc BC => EHC = 90 độ
Xét AEK vàHEC có:
EAK = EHC (= 90độ)(cmt)
AE = EH (cmt)
AEK = HEC (đối đỉnh)
=> AEK HEC (g.c.g)
=> EK = EC (2 cạnh tương ứng)
Xét HEC vuông tại H (vì EHC = 90 độ )
có EH < EC(cạnh huyền lớn hơn cạnh góc vuông)
Mà AE = EH (cmt) => AE < EC

Bạn tự vẽ hình nha!!!
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.

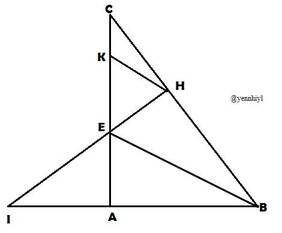
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE

tự vẽ hình nha!^^
1/a/ vì AB<AC(gt)\(\Rightarrow\)\(\widehat{B}< \widehat{C}\)(theo tính chất)
b)ta có:\(\widehat{BAH}+\widehat{AHB}+\widehat{B}=180\)độ
\(\widehat{CAH}+\widehat{AHC}+\widehat{C}=180\)độ
mà \(\widehat{B}< \widehat{C}\)(theo câu a)) và \(\widehat{AHB}=\widehat{AHC}=90\)độ
\(\Rightarrow\widehat{BAH}< \widehat{CAH}\)\(\Rightarrow HB< HC\)(tính chất)
2/a/\(Xét\Delta ABIva\Delta HBIcó:\)
góc BAI=BHI=90 độ
BỊ chung;góc B1=góc B2
Vậy \(\Delta ABI=\Delta HBI\left(ch-gn\right)\)
b/ vì IA=IH(do tgiac ABI=tgiac HBI)
Vậy tam giác AIH cân tại I
c/Vì AB=AH(do tam giác BIA= tam giác BIH)
\(\Rightarrow\)tam giác BAH cân tại B
mà BỊ là đường phân giác nên suy ra cũng là đường trung trực (theo tính chất của các đường trong tam giác cân)
\(\Rightarrow\)BI là đường trung trực của đoạn thẳng AH(đpcm)
Diễn giải:
- Khi cộng, trừ số thập phân ta tiến hành cộng hoặc trừ các phần tương ứng của các số đó.
Ví dụ 1:
Tính 0,25 + 2,5 ta làm như sau: 5 + 0 = 5 , 2 + 5 =7, 0 + 2 = 2. Vậy 0,25 + 2,5 = 2.75
Tính 8,6 - 2,7 ta làm như sau: 6 - 7 không trừ được ta lấy 16 - 7 = 9, tiếp tục 8 - 2 trừ thêm 1 nữa tức là 8 -3 = 5. Vậy 8,6 - 2,7 = 5,9
- Với phép nhân, chia các số thập phân ta cần viết chúng dưới dạng phân số.
1. Xét \(\Delta ABC\) vuông tại A có :
BC > AC ( ch > cgv) ; BC > AB .
2 . a) + b) Xét \(\Delta ABE\) và \(\Delta HBE\) có :
\(\widehat{BAC}=\widehat{EHB}=90^o;BE:chung;\widehat{ABE}=\widehat{HBE}\)
\(\Rightarrow\) \(\Delta ABE\) = \(\Delta HBE\) ( ch- gn)
\(\Rightarrow\) AB = HB
\(\Rightarrow\) \(\Delta ABH\) cân tại B mà BE là phân giác \(\Rightarrow\) BE là đường cao
\(\Rightarrow\) \(BE\perp AH\)
3.a) Xét \(\Delta ABC\) vuông tại A
\(\Rightarrow\) \(\widehat{ABC}+\widehat{BCA}=90^o\Rightarrow\widehat{ACB}=30^o\) ( 1 )
Có BE là phân giác \(\Rightarrow\) \(\widehat{ABE}=\widehat{EBC}=\frac{60^o}{2}=30^o\) (2)
Từ (1) và (2) \(\Rightarrow\) \(\Delta EBC\) cân tại E mà EH là đường cao \(\Rightarrow\) EH là trung tuyến hay BH = CH
b) Xét \(\Delta EHC\) vuông tại H
\(\Rightarrow\) \(EC>HC\left(ch>cgv\right)\)
mà AB = BH ; BH = HC \(\Rightarrow\) \(EC>AB\)