Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ 

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\left(x+y\right)^2=\left(\dfrac{1}{2}.2x+\dfrac{1}{3}.3y\right)^2\le\left(\dfrac{1}{4}+\dfrac{1}{9}\right)\left(4x^2+9y^2\right)=\dfrac{169}{36}\)
\(\Rightarrow-\dfrac{13}{6}\le x+y\le\dfrac{13}{6}\)
Dấu "=" lần lượt xảy ra tại \(\left(-\dfrac{3}{2};-\dfrac{2}{3}\right)\) và \(\left(\dfrac{3}{2};\dfrac{2}{3}\right)\)
2.
\(\left(y-2x\right)^2=\left(\dfrac{1}{4}.4y+\left(-\dfrac{1}{3}\right).6x\right)^2\le\left(\dfrac{1}{16}+\dfrac{1}{9}\right)\left(16y^2+36x^2\right)=\dfrac{25}{16}\)
\(\Rightarrow\left|y-2x\right|\le\dfrac{5}{4}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\mp\dfrac{2}{5};\pm\dfrac{9}{20}\right)\)
3.
\(B^2=\left(6.\sqrt{x-1}+8\sqrt{3-x}\right)^2\le\left(6^2+8^2\right)\left(x-1+3-x\right)=200\)
\(\Rightarrow B\le2\sqrt{10}\)
Dấu "=" xảy ra khi \(\dfrac{\sqrt{x-1}}{6}=\dfrac{\sqrt{3-x}}{8}\Leftrightarrow x=\dfrac{43}{25}\)
\(B=6\sqrt{x-1}+6\sqrt{3-x}+2\sqrt{3-x}\ge6\sqrt{x-1}+6\sqrt{3-x}\)
\(B\ge6\left(\sqrt{x-1}+\sqrt{3-x}\right)\ge6\sqrt{x-1+3-x}=6\sqrt{2}\)
\(B_{min}=6\sqrt{2}\) khi \(\sqrt{3-x}=0\Rightarrow x=3\)
4.
\(49=\left(3a+4b\right)^2=\left(\sqrt{3}.\sqrt{3}a+2.2b\right)^2\le\left(3+4\right)\left(3a^2+4b^2\right)\)
\(\Rightarrow3a^2+4b^2\ge\dfrac{49}{7}=7\)
Dấu "=" xảy ra khi \(a=b=1\)

5.
\(\sqrt{\left(a+b\right)\left(c+a\right)}\ge\sqrt{\left(\sqrt{ac}+\sqrt{ab}\right)^2}=\sqrt{ac}+\sqrt{ab}\)
\(\Rightarrow\dfrac{a}{a+\sqrt{\left(a+b\right)\left(a+c\right)}}\le\dfrac{a}{a+\sqrt{ac}+\sqrt{ab}}=\dfrac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Tương tự:
\(\dfrac{b}{b+\sqrt{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
\(\dfrac{c}{c+\sqrt{\left(a+c\right)\left(b+c\right)}}\le\dfrac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}\)
Cộng vế với vế:
\(P\le\dfrac{\sqrt{a}+\sqrt{b}+\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}=1\)
Dấu "=" xảy ra khi \(a=b=c\)
6.
\(P=\dfrac{a}{1+b-a}+\dfrac{b}{1+c-b}+\dfrac{c}{1+a-c}\)
Thay \(1=a+b+c\)
\(\Rightarrow P=\dfrac{a}{2b+c}+\dfrac{b}{2c+a}+\dfrac{c}{2a+b}\)
\(P=\dfrac{a^2}{2ab+ac}+\dfrac{b^2}{2bc+ab}+\dfrac{c^2}{2ac+bc}\)
\(P\ge\dfrac{\left(a+b+c\right)^2}{3ab+3bc+3ca}\ge\dfrac{3\left(ab+bc+ca\right)}{3\left(ab+bc+ca\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)

Thầy Nguyễn Việt Lâm ơi giúp em mấy bài này với.Em sắp phải nộp rồi ạ - Hoc24

Bài 6:
Xét ΔOAC vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)(hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBD
=>OC=OD
Bài 7:
a: Ta có: \(\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}+90^0=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}=90^0\)
mà \(\widehat{DAB}+\widehat{DBA}=90^0\)
nên \(\widehat{DBA}=\widehat{CAE}\)
Xét ΔABD vuông tại A và D và ΔCAE vuông tại E có
AB=AC
\(\widehat{DBA}=\widehat{EAC}\)
Do đó: ΔABD=ΔCAE
b: ta có: ΔABD=ΔCAE
=>DB=AE và AD=CE
DB+CE=DA+AE=DE

`<=> x(y - 2) + y - 2 + 3 = 0`
`<=> (x+1)(y-2) + 3 = 0`
`<=> (x+1)(y - 2) = -3`
`=> x + 1 in Ư(3)`
Đến đây chắc bạn tự làm được rồi ha, xét các ước của `x` và `y`.



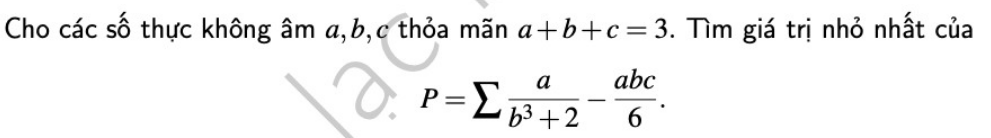
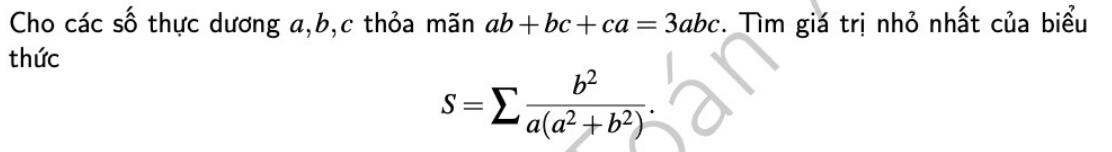








 Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người.
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 
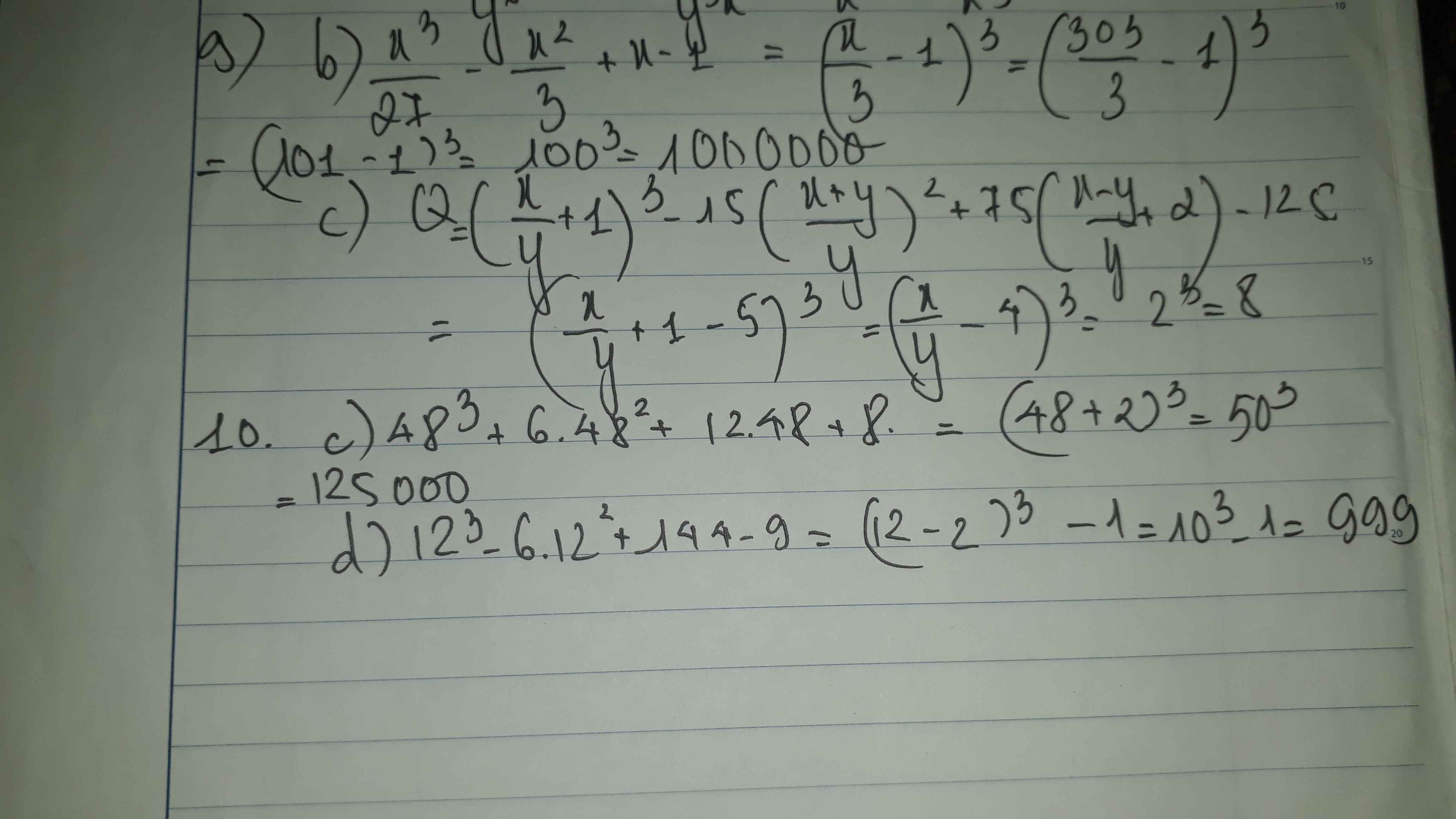



4.
\(ab+bc+ca=3abc\Leftrightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
\(S=\sum\dfrac{\dfrac{1}{y^2}}{\dfrac{1}{x}\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)}=\sum\dfrac{x^3}{x^2+y^2}=\sum\left(x-\dfrac{xy^2}{x^2+y^2}\right)\)
\(S\ge\sum\left(x-\dfrac{xy^2}{2xy}\right)=\sum\left(x-\dfrac{y}{2}\right)=\dfrac{x+y+z}{2}=\dfrac{3}{2}\)
\(S_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
5.
Đặt \(\left(\dfrac{1}{a};\dfrac{2}{b};\dfrac{3}{c}\right)=\left(x;y;z\right)\Rightarrow x+y+z=3\)
Đặt vế trái là P
\(P=\dfrac{z^3}{x^2+z^2}+\dfrac{x^3}{x^2+y^2}+\dfrac{y^3}{y^2+z^2}\)
Quay lại dòng 3 của bài số 4