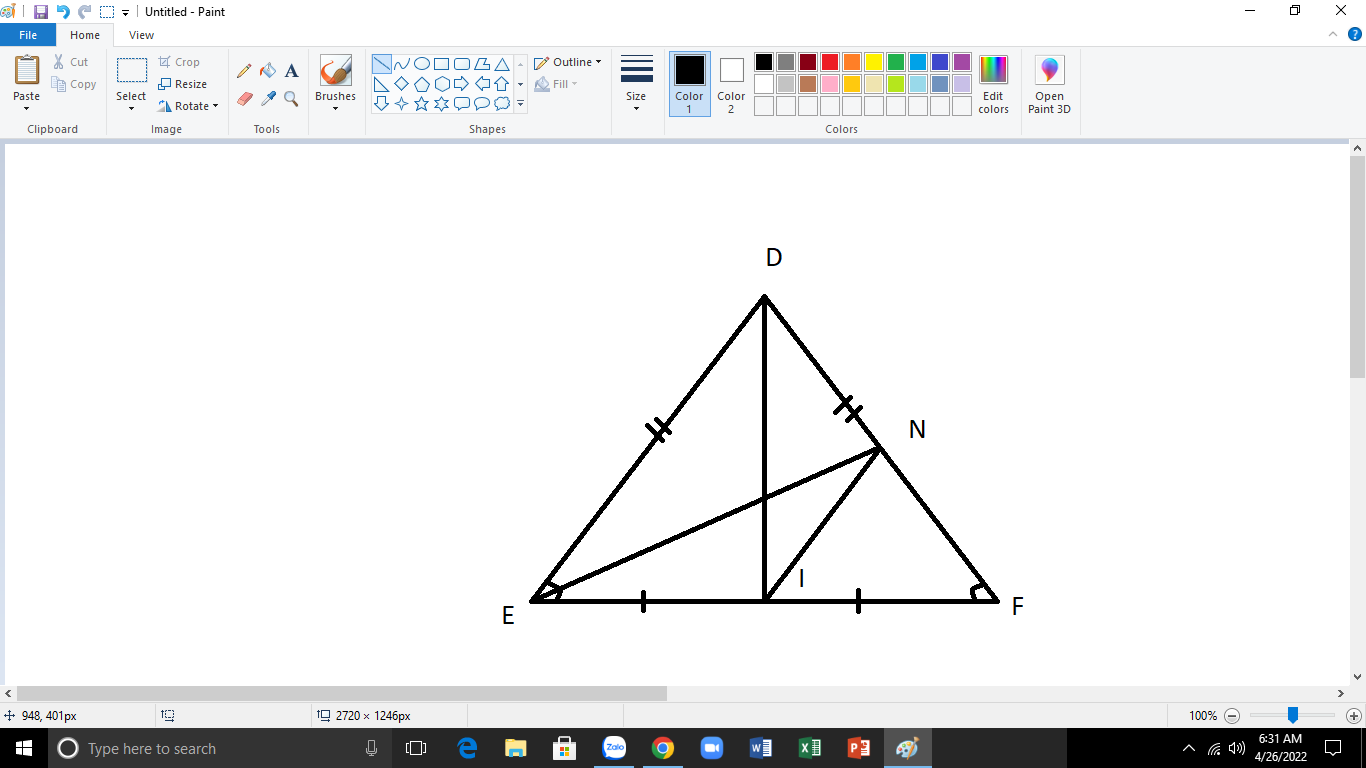
Cho tam giác DEF cân tại D với đường trung tuyến DI
a)CM:Tam giác DEI=Tam giác DFI
b)CM:DI vuông góc EF
c)Kẻ đường trung tuyến EN.Chứng minh rằng:IN song song với ED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 6 2023
a: Sửa đề: ΔDEF cân tại D
Xét ΔDEI và ΔDFI có
DE=DF
EI=FI
DI chung
=>ΔDEI=ΔDFI
b: ΔDEF cân tại D
mà DI là trung tuyến
nên DI là trung trực của EF
c: Xét ΔDEF có I,N lần lượt là trung điểm của FE,FD
=>IN là đường trung bình
=>IN//DE
11 tháng 4 2018
â)Xét tam giác DEI và tam giác DFI có
DI là cạnh chung
DE=DF(tam giác DEF cân)
IE=IF(DI là trung tuyến)
=>Tam giác DEI = tam giác DFI(c.c.c)
=>DIE=DIF(2 góc tương ứng)
Ta có :DIE+DIF=180o
=>DIE=DIF=\(\frac{180^0}{2}\)=900
=>DI vuông EF
c)Ta có :EN là đường trung tuyến
Nên ND=NF nên IN là đường trung tuyến của tam giác vuông DIF
Trên tia dối của tia IN lấy M sao cho NM=NI
Ta sẽ chứng minh được tam giác DNI=tam giác FNM(c.g.c)
=>DI=EF (2 cạnh tương ứng)
Vì góc DIn=góc NMF ở vị trí so le trong
=>IN//ED
11 tháng 4 2018
a) Xét\(\Delta EDI\) và \(\Delta FDI\) ,có
EI=FI(vì ID là đường trung tuyến của tam giácDEF)
ID chung
ED=DF(vì tam giác DEF cân tại D)
\(\Rightarrow\) \(\Delta EDI=\Delta FDI\)(c-c-c)
b) Vì ID là đường trung tuyến của tam giác DEF
\(\Rightarrow\)ID là đường phân giác,đồng thời là đường cao
\(\Rightarrow\)ID vuông góc vs EF
2 tháng 4 2022
a: Xét ΔDEI và ΔDFI có
DE=DF
EI=FI
DI chung
Do đó: ΔDEI=ΔDFI
b: Ta có: ΔDEF cân tại D
mà DI là đường trung tuyến
nên DI là đường cao
22 tháng 5 2021
bn tham khỏa đường link này nha /hoi-dap/detail/220486054053.html
19 tháng 4 2022
a.Xét tam giác DEI và tam giác DFI, có:
^E = ^F ( DEF cân )
DE = DF ( DEF cân )
EI = FI ( gt )
Vậy tam giác DEI = tam giác DFI ( c.g.c )
b.Ta có: DI là đường trung tuyến trong tam giác cân DEF
=>DI vuông góc EF
c.Ta có: DN = FN ( gt )
EI = FI ( gt )
=> IN là đường trung bình của tam giác DEF
=> IN//ED
DEI =
29 tháng 7 2023
a: Xét ΔDEI và ΔDFI có
DE=DF
EI=FI
DI chung
=>ΔDEI=ΔDFI
b: ΔDEF cân tại D
mà DI là trung tuyến
nên DI vuông góc EF
c: Xét ΔDFE có FI/FE=FN/FD
nên IN//ED
26 tháng 4 2022
\(\text{a)Xét }\Delta DEI\text{ và }\Delta DFI\text{ có:}\)
\(DE=DF\left(\Delta DÈ\text{ cân tại D}\right)\)
\(\widehat{DEF}=\widehat{DFE}\left(\Delta DEF\text{ cân tại D}\right)\)
\(DI\text{ chung}\)
\(\Rightarrow\Delta DEI=\Delta DFI\left(c-g-c\right)\)
\(\text{b)Vì }\Delta DEI=\Delta DFI\left(cmt\right)\)
\(\Rightarrow\widehat{DIE}=\widehat{DIF}\left(\text{hai góc tương ứng}\right)\)
\(\text{Mà chúng kề bù}\)
\(\Rightarrow\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)
\(\Rightarrow DI\perp EF\)
\(\text{c)K bt sorry}\)
26 tháng 4 2022
Mik vẽ trên máy nó k chính xác lắm có vãi chỗ bị lệch bn thông cảm
9 tháng 5 2015
chắc câu a và b bạn đả giải dc nên mình chỉ trinh bày câu c
bạn tự vẽ hình nha
c)en là đường trung tuyến của tam giác def nên nd=nf suy ra in là đường trung tuyến của tam giác dif
trên tia đối của tia ni , vẽ diểm t sao cho nt=ni
cmđ:tam giac dni=fnt(c.g.c)
suy ra di =tf(2ctu)và góc din=ftn mà 2 góc này ở vị trí so le trong nên di song song với tf suy ra góc die=tfi =90 độ
cmđ tam giác dif =tfi (c.g.c) suy ra df =ti (2 cạnh tương ứng) suy ra df/2=ti/2 nên dn=nf=ni=nt
ni=nf suy ra tam giác inf cân tại n nên góc nif =nfi mà dfi =dei (tam giác def cân tại d) nên góc nif=dei
và :2 góc này ở vị trí đồng vị
nên in song song với de