Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.a) Tính độ dìa AC khi AB= 9cm, BC= 15cmb) Chứng minh: Tam giác ABD=tam giác EBDc) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC când) Chứng minh: AD<DCBài 2: Cho tam giác ABC vuông tại A có AB= 12cm, AC= 16cm.Kẻ BF là đường trung tuyến của tam...
Đọc tiếp
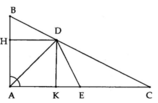
Bài 1: Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE=BA. Qua E kẻ đường thẳng d vuông góc với BC và d cắt AC tại D.
a) Tính độ dìa AC khi AB= 9cm, BC= 15cm
b) Chứng minh: Tam giác ABD=tam giác EBD
c) Gọi H là giao điểm của đường thẳng AB và đường thẳng d. Chứng minh tam giác HBC cân
d) Chứng minh: AD<DC
Bài 2: Cho tam giác ABC vuông tại A có AB= 12cm, AC= 16cm.Kẻ BF là đường trung tuyến của tam giác ABC. Từ điểm C kẻ đường thẳng vuông góc với AC cắt đường trung tuyến BF tại D
a) Tính độ dài BC?
b) Chứng minh rằng: Tam giác ABF=tam giác CDF
c) Chứng minh: BF<(AB+BC):2
Bài 3: Cho tam giacsABC vuông tại A; tia phân giác của góc B cắt AC tại D. Kẻ DH vuông góc với BC\(\left(H\in BC\right)\). Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 9cm, AC= 12cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh: Tam giác KDC cân
d) Chứng minh: AB+AC>BD+DC
Bài 4: Cho tam giác ABC vuông tại A. Trên tia BC lấy điểm H sao cho BH=BA. Tia phân giác của góc B cắt AC tại D. Gọi K là giao điểm của AB và DH
a) Tính độ dài BC khi AB= 3cm, AC= 4cm
b) Chứng minh: Tam giác ABD=tam giác HBD
c) Chứng minh \(Dh\perp BC\)
d) So sánh DH với DK


a: AC=căn 5^2-3^2=4cm
b: Đề bài yêu cầu gì vậy bạn?
c: Xét ΔCDE có
CK vừa là đường cao, vừa là trung tuyến
=>ΔCDE cân tại C
=>góc CED=góc CDE
mà góc CDE=góc ADB
nên góc CEK=góc ADB