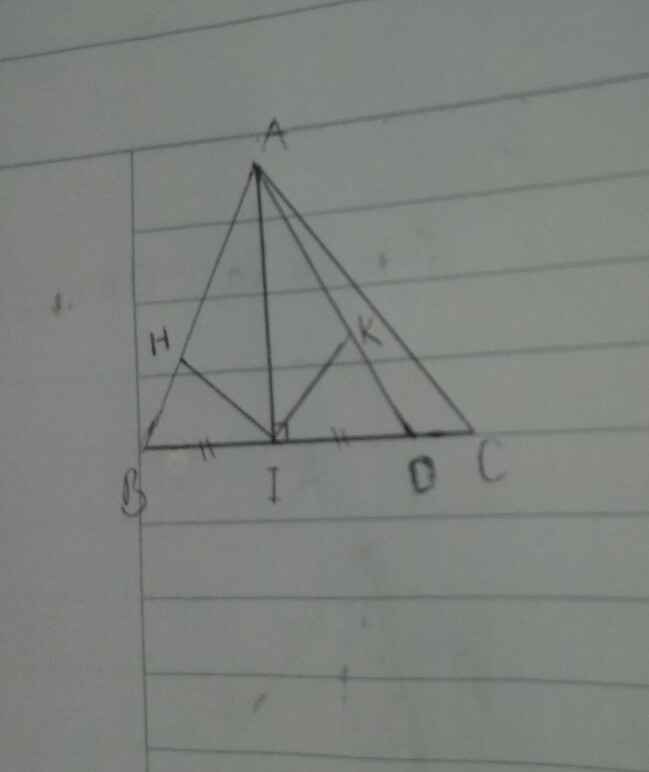
Cho D ABC nhọn (AB <AC) nội tiếp đường tròn (O), Ba đường cao AD;BE; CF cắt nhau tại H. Hai đường cao BE; CF lần lượt cắt đường tròn tại điểm thứ hai là M và N. FD cắt BH tại K
1) So sánh cung AB và cung AC
2) Cho ∠ADB = 550 Tính số đo cung BC
3) Chứng minh tứ giác AEHF nội tiếp
4)Chứng minh MN//EF
5) Chứng minh HE.KB = EF.KD
6*) Cho BC cố định, A chạy trên cung lớn BC. Chứng minh độ dài AH; EF không đổi

1: AB<AC
=>góc C<góc B
Xét (O) có
góc ACB=1/2*sđ cung AB
góc ABC=1/2*sđ cung AC
mà góc ACB<góc ABC
nên sđ cung AB<sđ cung AC
3: góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
4:
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc HFE=góc HBC
=>góc HFE=góc HNM
mà hai góc này ở vị trí đồng vị
nên FE//MN