giúp mình câu d với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)

d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC

`d)\sqrt{2+\sqrt{2+\sqrt{x}}}=2` `ĐK: x >= 0`
`=>2+\sqrt{2+\sqrt{x}}=4`
`=>\sqrt{2+\sqrt{x}}=2`
`=>2+\sqrt{x}=4`
`=>\sqrt{x}=2`
`=>x=4` (t/m)
Vậy `x=4`

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB và AD/AB=AE/AC
=>ΔADE đồng dạng vơi ΔABC
=>góc ABC=góc ADE
b: Xét ΔHEB vuông tại E và ΔHDC vuôg tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HD*HB và HE/HB=HD/HC
=>ΔHED đồng dạng với ΔHBC
d: ΔABC đều
=>H là trọng tâm
=>HD=1/3BD=\(\dfrac{1}{3}\cdot\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\) và \(HE=\dfrac{1}{3}CE=\dfrac{a\sqrt{3}}{6}\)
\(S_{HED}=\dfrac{1}{2}\cdot HE\cdot HD\cdot sinEHD\)
\(=\dfrac{1}{2}\cdot sin120\cdot\dfrac{a\sqrt{3}}{6}\cdot\dfrac{a\sqrt{3}}{6}=\dfrac{\sqrt{3}}{48}\cdot a^2\)
\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(\dfrac{S_{HED}}{S_{BAC}}=\dfrac{\sqrt{3}}{48}:\dfrac{\sqrt{3}}{4}=\dfrac{1}{12}\)
Cậu giải thích cho mình này nghĩa là gì được không, mình không biết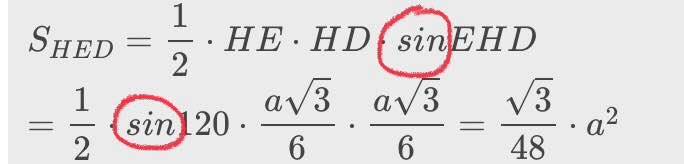

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB và AD/AB=AE/AC
=>ΔADE đồng dạng vơi ΔABC
=>góc ABC=góc ADE
b: Xét ΔHEB vuông tại E và ΔHDC vuôg tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HD*HB và HE/HB=HD/HC
=>ΔHED đồng dạng với ΔHBC
d: ΔABC đều
=>H là trọng tâm
=>HD=1/3BD=\(\dfrac{1}{3}\cdot\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{6}\) và \(HE=\dfrac{1}{3}CE=\dfrac{a\sqrt{3}}{6}\)
\(S_{HED}=\dfrac{1}{2}\cdot HE\cdot HD\cdot sinEHD\)
\(=\dfrac{1}{2}\cdot sin120\cdot\dfrac{a\sqrt{3}}{6}\cdot\dfrac{a\sqrt{3}}{6}=\dfrac{\sqrt{3}}{48}\cdot a^2\)
\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(\dfrac{S_{HED}}{S_{BAC}}=\dfrac{\sqrt{3}}{48}:\dfrac{\sqrt{3}}{4}=\dfrac{1}{12}\)

d) Gọi x,y lần lượt là số mol Al, Fe
\(\left\{{}\begin{matrix}27x+56y=8,3\\1,5x+y=0,25\end{matrix}\right.\)
=> x=0,1 ; y=0,1
Kết tủa : Al(OH)3, Fe(OH)2
Bảo toàn nguyên tố Al: \(n_{Al\left(OH\right)_3}=n_{Al}=0,1\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{Fe\left(OH\right)_2}=n_{Fe}=0,1\left(mol\right)\)
=> \(m=0,1.78+0,1.90=16,8\left(g\right)\)
Nung kết tủa thu được chất rắn : Al2O3 và FeO
Bảo toàn nguyên tố Al: \(n_{Al_2O_3}.2=n_{Al}\Rightarrow n_{Al_2O_3}=0,05\left(mol\right)\)
Bảo toàn nguyên tố Fe: \(n_{FeO}=n_{Fe}=0,1\left(mol\right)\)
=> \(a=0,05.102+0,1.72=12,3\left(g\right)\)
