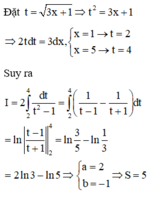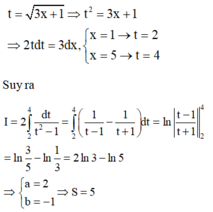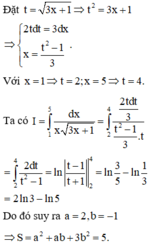ab = 3b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
29 tháng 12 2023
Lời giải:
$a^2-2ab-3b^2\geq 0$
$\Leftrightarrow (a^2+ab)-(3ab+3b^2)\geq 0$
$\Leftrightarrow a(a+b)-3b(a+b)\geq 0$
$\Leftrightarrow (a+b)(a-3b)\geq 0$
$\Leftrightarrow a-3b\geq 0$ (do $a+b>0$ với mọi $a,b>0$)
$\Leftrightarrow a\geq 3b$
Xét hiệu:
$P-\frac{37}{3}=\frac{4a^2+b^2}{ab}-\frac{37}{3}$
$=\frac{12a^2+3b^2-37ab}{3ab}=\frac{(a-3b)(12a-b)}{3ab}\geq 0$ do $a\geq 3b>0$
$\Rightarrow P\geq \frac{37}{3}$
Vậy $P_{\min}=\frac{37}{3}$
CM
3 tháng 1 2018
Chọn D.
Đặt t = 3 x + 1 → t 2 = 3 x + 1 ⇒ d x = 2 3 t d t x = t 2 - 1 2 Đổi cận x = 1 → t = 2 x = 5 → t = 4
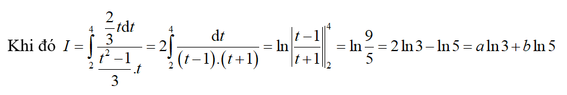
Suy ra a = 2; b = -1 ⇒ a2 + ab + 3b2 = 5.
NN
1
5 tháng 7 2023
\(\left(3b^2\right)^2-b^3.\left(1-5b\right)\)
\(=9b^4-b^3+5b^4\)
\(=14b^4-b^3\)
C
2
8 tháng 8 2021
\(5a^2-14ab-3b^2\\ =5a^2-15ab-ab-3b^2\\ =5a\left(a-3b\right)-b\left(a-3b\right)\\ =\left(5a-b\right)\left(a-3b\right)\)
8 tháng 8 2021
\(5a^2-14ab-3b^2\)
\(=5a^2-15ab+ab-3b^2\)
\(=5a\left(a-3b\right)+b\left(a-3b\right)\)
\(=\left(a-3b\right)\left(5a+b\right)\)