Giúp mình vớiiii
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y=\dfrac{2\left(2cos^2x-1\right)+3sin2x+3}{3-sin2x+cos2x}=\dfrac{3sin2x+2cos2x+3}{3-sin2x+cos2x}\left(\cdot\right)\)
\(\left(\cdot\right)\Leftrightarrow y\left(3-sin2x+cos2x\right)=3sin2x+2cos2x+3\)
\(\Leftrightarrow\left(y+3\right)sin2x+\left(2-y\right)cos2x=3y-3\left(1\right)\)
Để phương trình (1) có nghiệm thì:
\(\left(y+3\right)^2+\left(2-y\right)^2\ge\left(3y-3\right)^2\)
\(\Leftrightarrow7y^2-20y-4\le0\)
\(\Leftrightarrow\dfrac{10-8\sqrt{2}}{7}\le y\le\dfrac{10+8\sqrt{2}}{7}\)
=> min, max của y

Lời giải:
Xét hàm $f(x)=(-4m+3)x^3+4mx-1$ liên tục trên $R$
$f(1)=-4m+3+4m-1=2>0$
$f(-1)=4m-3-4m-1=-4<0$
$\Rightarrow f(1)f(-1)<0$
Do đó pt $f(x)=0$ luôn có ít nhất 1 nghiệm thuộc $(-1;1)$ với mọi $m$ (đpcm)

Olm chào em. Em gặp phải chuyện gì vậy, hay em cần giải bài tập nào? Em hãy yêu cầu cụ thể để được trợ giúp nhé


Quy ước :
A : quy định tính trạng thân cao.
a : quy định tính trạng thân thấp.
B : quy định tính trạng quả đỏ.
b : quy định tính trạng quả vàng.
Cho cà chua thân cao, quả đỏ thuần chủng lai với cà chua thân thấp, quả vàng thu được F1.
=> P có KG là : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng).
* Sơ đồ lai :
P : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng)
G : AB ab
F1 : AaBb ( 100 % thân cao quả đỏ ).
Quy ước :
A : quy định tính trạng thân cao.
a : quy định tính trạng thân thấp.
B : quy định tính trạng quả đỏ.
b : quy định tính trạng quả vàng.
Cho cà chua thân cao, quả đỏ thuần chủng lai với cà chua thân thấp, quả vàng thu được F1.
=> P có KG là : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng).
* Sơ đồ lai :
P : AABB( thân cao, quả đỏ ) x aabb(thân thấp, quả vàng)
G : AB ab
F1 : AaBb ( 100 % thân cao quả đỏ ).



\(b,\text{PT hoành độ giao điểm: }3x-1=x+2\\ \Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow y=\dfrac{7}{2}\Leftrightarrow A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\\ \text{Vậy }A\left(\dfrac{3}{2};\dfrac{7}{2}\right)\text{ là giao 2 đths}\\ c,\left(D_2\right)\text{//}\left(D\right);B\left(1;0\right)\in\left(D_2\right)\Leftrightarrow\left\{{}\begin{matrix}a+b=0\\a=3;b\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-3\end{matrix}\right.\\ \Leftrightarrow\left(D_2\right):y=3x-3\)

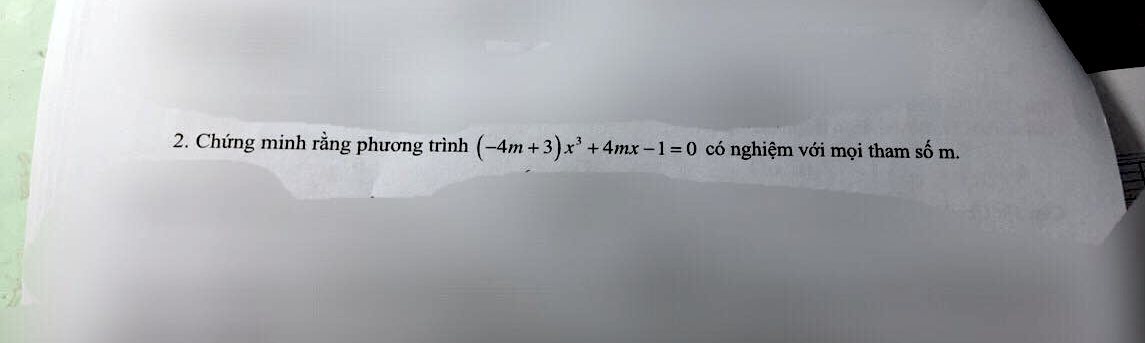
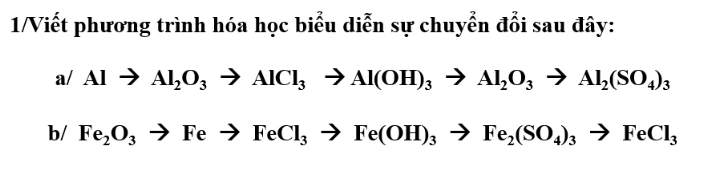

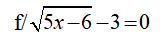


Tổng đã cho là tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{u_1}{1-q}=\dfrac{1}{1-\dfrac{1}{2}}=2\)