Giải giúp em câu 1, câu 2, câu 4 với ạ em cảm ơn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LP
2
Những câu hỏi liên quan
24 tháng 7 2021
18) Ta có: \(H=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}+1\right)-\left(2\sqrt{x}-1\right)\)
\(=x+\sqrt{x}-2\sqrt{x}+1\)
\(=x-\sqrt{x}+1\)
19) Ta có: \(T=\dfrac{a-3\sqrt{a}-4}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}-4\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-4\)
NH
0
NH
1
12 tháng 1 2022
Câu 19:
\(=\dfrac{11x+x-18}{2x-3}=\dfrac{12x-18}{2x-3}=6\)
Câu 20:
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}=\dfrac{x-5}{5x}\)
TN
1
18 tháng 1 2023
\(lim\left(\sqrt[3]{n^3+4}-\sqrt[3]{n^3-1}\right)\)
\(=lim\left(\sqrt[3]{1+\dfrac{4}{n^3}}-\sqrt[3]{1-\dfrac{1}{n^3}}\right)=\sqrt[3]{1}-\sqrt[3]{1}=0\)
TH
1
8 tháng 2 2022
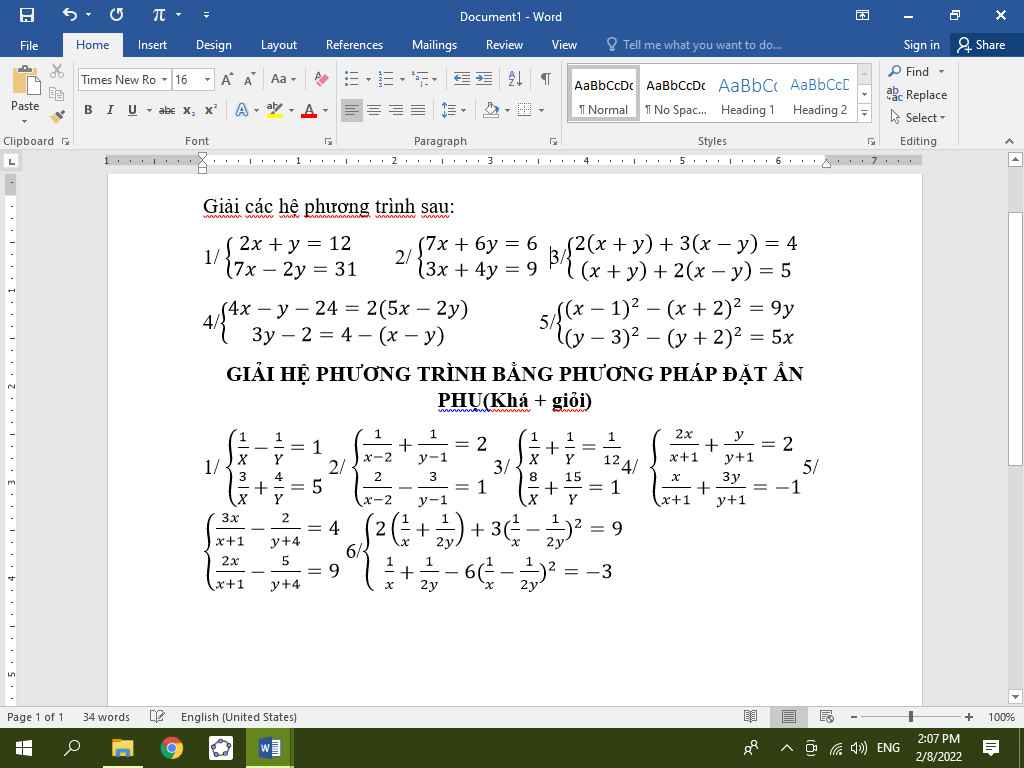
1, \(\left\{{}\begin{matrix}4x+2y=24\\7x-2y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=55\\y=12-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)
2, thiếu đề
4, \(\left\{{}\begin{matrix}4x-y-24=10x-4y\\3y-2=4-x+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\-6x-12y=-36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15y=60\\x=6-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-2\end{matrix}\right.\)
NV
2
16 tháng 3 2021
Câu 4:
a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
VV
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
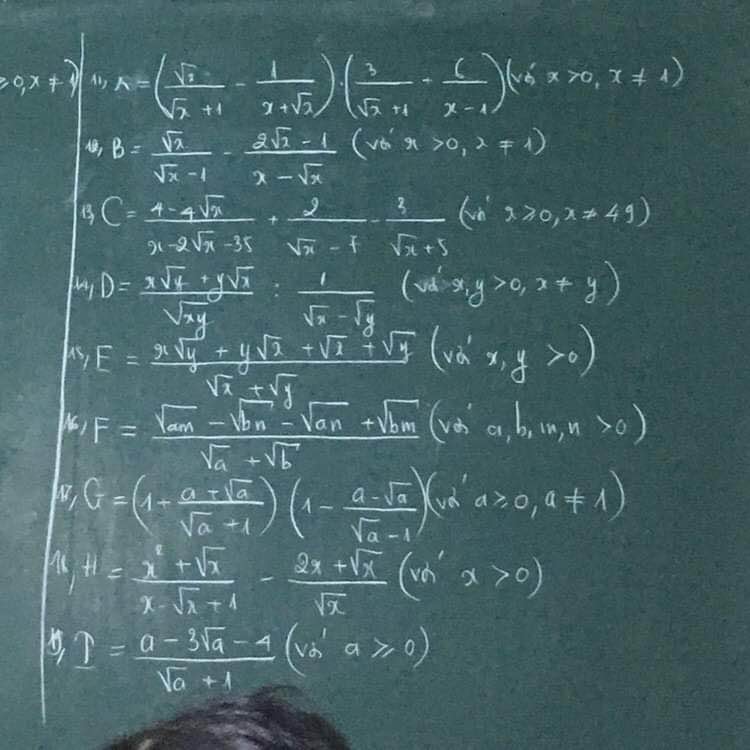
2.
Áp dụng định lý hàm cosin:
\(b=\sqrt{a^2+c^2-2ac.cosB}=\sqrt{8^2+3^2-2.8.3.cos60^0}=7\)
\(S_{ABC}=\dfrac{1}{2}ac.sinB=\dfrac{1}{2}.8.3.sin60^0=6\sqrt{3}\)
4.
\(\Delta=\left(m+2\right)^2-16>0\Leftrightarrow m^2+4m-12>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -6\end{matrix}\right.\) (1)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-m-2\\x_1x_2=4\end{matrix}\right.\)
\(x_1+x_2+x_1x_2>1\)
\(\Leftrightarrow-m-2+4>1\)
\(\Rightarrow m< 1\) (2)
Kết hợp (1); (2) ta được \(m< -6\)