GIÚP MIK VS
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
0
DT
0
M
1
4 tháng 4 2023
27. unforgetable
câu 31 đổi thành ...if I can give him his guide....
câu 32 thiếu on trong turned on và đổi thành has been turned on vì câu gốc là HTHT
câu 33 rút gọn mệnh đề ok
câu 34 hơi phân vân nhưng mình thấy đúng
TK
1
17 tháng 10 2021
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
TK
1
P
1
22 tháng 10 2021
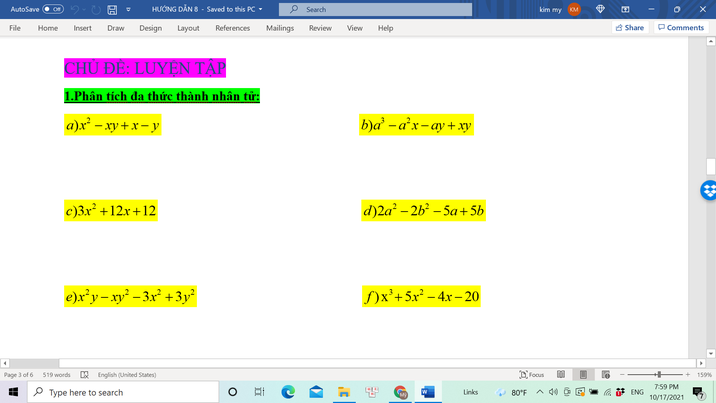
a) \(=x\left(x-y\right)+\left(x-y\right)=\left(x-y\right)\left(x+1\right)\)
b) \(=a^2\left(a-x\right)-y\left(a-x\right)=\left(a-x\right)\left(a^2-y\right)\)
c) \(=3\left(x^2+4x+4\right)=3\left(x+2\right)^2\)
d) \(=2\left(a^2-b^2\right)-5\left(a-b\right)=2\left(a-b\right)\left(a+b\right)-5\left(a-b\right)\)
\(=\left(a-b\right)\left(2a+2b+5\right)\)
e) \(=xy\left(x-y\right)-3\left(x^2-y^2\right)=xy\left(x-y\right)-3\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(xy-3x-3y\right)\)
f) \(=x^2\left(x+5\right)-4\left(x+5\right)=\left(x+5\right)\left(x^2-4\right)\)
\(=\left(x+5\right)\left(x-2\right)\left(x+2\right)\)
NL
2
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 1 2022
\(3x\left(x-y\right)+x-y\)
\(=3x\left(x-y\right)+1\left(x-y\right)\)
\(=\left(x-y\right)\left(3x+1\right)\)
26 tháng 2 2022
1 didn't
2 did
3 doesn't
4 does
5 don't
6 do
7 did
8 doesn't
26 tháng 2 2022
1. a little
2. much
3. many
4. a few
5. many
6. much
7. a little
8. a few
k mik nha bn
\(\sqrt{2x^3+3x^2+6x+16}-\sqrt{4-x}\ge2\sqrt{3}\) (ĐK: \(-2\le x\le4\)
\(\Leftrightarrow\sqrt{2x^3+3x^2+6x+16}\ge2\sqrt{3}+\sqrt{4-x}\)
\(\Leftrightarrow2x^3+3x^2+6x+16\ge12+4-x+4\sqrt{3\left(4-x\right)}\)
\(\Leftrightarrow2x^3+3x^2+7x\ge4\sqrt{3\left(4-x\right)}\)
\(\Leftrightarrow\hept{\begin{cases}\left(2x^3+3x^2+7x\right)^2\ge48\left(4-x\right)\\2x^3+3x^2+7x\ge0\end{cases}}\)
\(\Leftrightarrow\left(x-1\right)\left(4x^5+16x^4+53x^3+95x^2+144x+192\right)\ge0\)(\(x\ge0\))
\(\Leftrightarrow x-1\ge0\)(vì \(x\ge0\))
\(\Leftrightarrow x\ge1\)
Vậy bất phương trình có tập nghiệm là \(\left[1;4\right]\).
\(a^2+b^2=1^2+4^2=17\)
ĐKXĐ: \(-2\le x\le4\)
\(\sqrt{2x^3+3x^2+6x+16}\ge\sqrt{4-x}+2\sqrt{3}\)
\(\Leftrightarrow2x^3+3x^2+6x+16\ge16-x+4\sqrt{3\left(4-x\right)}\)
\(\Leftrightarrow2x^3+3x^2+7x\ge4\sqrt{3\left(4-x\right)}\)
\(\Leftrightarrow2x^3+3x^2+7x-12+4\left(3-\sqrt{3\left(4-x\right)}\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+5x+12\right)+\dfrac{12\left(x-1\right)}{3+\sqrt{3\left(4-x\right)}}\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+5x+12+\dfrac{12}{3+\sqrt{3\left(4-x\right)}}\right)\ge0\)
Do \(2x^2+5x+12+\dfrac{12}{3+\sqrt{3\left(4-x\right)}}>0\) với mọi x nên BPT tương đương:
\(x-1\ge0\Rightarrow x\ge1\)
\(\Rightarrow1\le x\le4\Rightarrow a^2+b^2=17\)