1/Tìm GTNN của
M= 4x2-4x + 5
N= 9x2 + 5x
2/ Chứng tỏ biểu thức sau luôn dương với mọi x
A= x2-6x + 12
B= 4x2 -3x +5
Nhờ các bạn giải giùm mk ạ!!!!!!!!!!!!
Thank cấc bạn nhìu!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. $-x^2-2x-8=-7-(x^2+2x+1)=-7-(x+1)^2$
Vì $(x+1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên
$-x^2-2x-8=-7-(x+1)^2\leq -7< 0$ với mọi $x\in\mathbb{R}$
Vậy biểu thức luôn nhận giá trị âm với mọi $x$
b.
$-x^2-5x-11=-11+2,5^2-(x^2+5x+2,5^2)< -11+3^2-(x+2,5)^2$
$=-2-(x+2,5)^2\leq -2< 0$ với mọi $x\in\mathbb{R}$ (đpcm)
c.
$-4x^2-4x-2=-1-(4x^2+4x+1)=-1-(2x+1)^2\leq -1< 0$ với mọi $x\in\mathbb{R}$ (đpcm)
d.
$-9x^2+6x-7=-6-(9x^2-6x+1)=-6-(3x-1)^2\leq -6< 0$ với mọi $x\in\mathbb{R}$ (đpcm)

a: ta có: \(A=x^2-3x+10\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{31}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{31}{4}>0\forall x\)
b: Ta có: \(B=x^2-5x+2021\)
\(=x^2-2\cdot x\cdot\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{8015}{4}\)
\(=\left(x-\dfrac{5}{2}\right)^2+\dfrac{8015}{4}>0\forall x\)

a) \(9x^2-6x+11=\left(3x\right)^2-2.3x+1+10=\left(3x-1\right)^2+10>0\forall x\)
b) \(3x^2-12x+81=3.\left(x^2-4x+9\right)=3.\left(x-2\right)^2+15>0\forall x\)
c) \(5x^2-5x+4=5.\left(x^2-x+\dfrac{4}{5}\right)=5.\left(x^2-x+\dfrac{1}{4}+\dfrac{11}{20}\right)=5.\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
d) \(2x^2-2x+9=2.\left(x^2-x+\dfrac{9}{2}\right)=2.\left(x-\dfrac{1}{2}\right)^2+\dfrac{17}{2}>0\forall x\)

Chọn A
Tam thức : -4x2+ 5x-1 có a= -4 và ∆ = -7< 0
suy ra -4x2+ 5x-1<0 với mọi x
Do đó h(x) luôn dương khi và chỉ khi
f(x) = -x2+ 4( m+1) x+ 1- 4m2 luôn âm
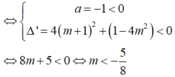
Vậy với m< -5/8 thì biểu thức h(x) luôn dương.

a, P(x)=(2x^3-x^3)+x^2+(3x-2x)+2=x^3+x^2+x+2
Q(x)=(3x^3-4x^3)+(5x^2-4x^2)+(3x-4x)+1=-x^3+x^2-x+1
b, M(x)=P(x)+Q(x)=x^3+x^2+x+2+(-x^3)+x^2-x+1=2x^2+3
N(x)=P(x)-Q(x)=x^3+x^2+x+2-(-x^3+x^2-x+1)=2x^3+2x+1
c, M(x)=2x^2+3
do x^2>=0 với mọi x=2x^2>=0
nên 2x^2+3>=3 với mọi x
để M(x) có nghiệm thì phải tồn tại x để M(x)=0 ( vô lý vì M(x)>=3 với mọi x)
do đó đa thức M(x) không có nghiệm

1.
Đặt \(x-2=t\ne0\Rightarrow x=t+2\)
\(B=\dfrac{4\left(t+2\right)^2-6\left(t+2\right)+1}{t^2}=\dfrac{4t^2+10t+5}{t^2}=\dfrac{5}{t^2}+\dfrac{2}{t}+4=5\left(\dfrac{1}{t}+\dfrac{1}{5}\right)^2+\dfrac{19}{5}\ge\dfrac{19}{5}\)
\(B_{min}=\dfrac{19}{5}\) khi \(t=-5\) hay \(x=-3\)
2.
Đặt \(x-1=t\ne0\Rightarrow x=t+1\)
\(C=\dfrac{\left(t+1\right)^2+4\left(t+1\right)-14}{t^2}=\dfrac{t^2+6t-9}{t^2}=-\dfrac{9}{t^2}+\dfrac{6}{t}+1=-\left(\dfrac{3}{t}-1\right)^2+2\le2\)
\(C_{max}=2\) khi \(t=3\) hay \(x=4\)
\(M=4x^2-4x+1+4=\left(2x-1\right)^2+4\)
vì (2x-1)^2 >= 0 => M >= 4
dầu "=" xảy ra <=> 2x-1=0<=>x=1/2
tương tự nhé
2. b B=4(x^2+3/4x+5/4)
Bài 1:
a)M= 4x2-4x + 5
=4x2-4x+1+4
=(2x-1)2+4
Ta thấy:(2x-1)2+4\(\ge\)0+4=4
Dấu = khi x=1/2
Vậy.....
b)N= 9x2 + 5x
\(=9\left(x+\frac{5}{18}\right)^2-\frac{25}{36}\)
Ta thấy:\(9\left(x+\frac{5}{18}\right)^2-\frac{25}{36}\ge0-\frac{25}{36}=-\frac{25}{36}\)
Dấu = khi x=-5/18
Vậy...
Bài 2:
a)A= x2-6x + 12
=x2-6x+9+3
=(x-3)2+3 >0 với mọi x (Đpcm)
b)B= 4x2 -3x +5
\(=4\left(x-\frac{3}{8}\right)^2+\frac{71}{16}>0\)với mọi x (Đpcm)