mình cần lời giải chi tiết ạ :((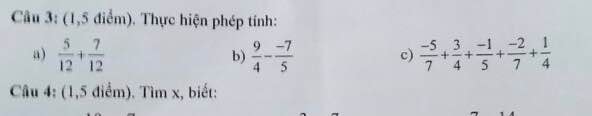
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2
a) \(=x\left(3x^3-x^2+5\right)\)
b) \(=\left(2x+3y\right)\left(x-y\right)\)
c) \(=\left(x^2-3x\right)-\left(4x-12\right)=x\left(x-3\right)-4\left(x-3\right)=\left(x-3\right)\left(x-4\right)\)
a, = x.(3x3 - x2 + 5)
b, = 2x.(x - y) + 3y.(x - y) = (x - y).(2x + 3y)
c, = x2 - 3x - 4x + 12 = (x2 - 3x) - (4x - 12) = x.(x - 3) - 4.(x - 3) = (x - 3).(x - 4)

\(9,\dfrac{x^2-81}{10x^2-90x}=\dfrac{\left(x-9\right)\left(x+9\right)}{10x\left(x-9\right)}=\dfrac{x+9}{10x}\Rightarrow M=10x\\ 10,\dfrac{2x^2+3x}{4x^2-9}=\dfrac{x\left(2x+3\right)}{\left(2x-3\right)\left(2x+3\right)}=\dfrac{x}{2x-3}\Rightarrow A=x\)
\(9,M=\dfrac{\left(x+9\right)\left(10x^2-90x\right)}{x^2-81}=\dfrac{10x\left(x+9\right)\left(x-9\right)}{\left(x-9\right)\left(x+9\right)}=10x\\ 10,A=\dfrac{\left(2x-3\right)\left(2x^2+3x\right)}{4x^2-9}=\dfrac{x\left(2x+3\right)\left(2x-3\right)}{\left(2x-3\right)\left(2x+3\right)}=x\)

Chu vi đáy của viên phấn là \(3,14cm\)
Ta có : \(C=R.2.3,14=R.6,28\Rightarrow R=\dfrac{C}{6,28}=\dfrac{3,14}{6,28}=0,5\left(cm\right)\)
Thể tích của 1 viên phấn là :
\(V=3,14.R^2.h=3,14.0,5^2.12=9,42\left(cm^3\right)\)
Thể tích của 20 viên phấn là : \(9,42.20=188,4\left(cm^3\right)\)
Phần không gian bên trong hộp là :
\(200-188,4=11,6\left(cm^3\right)\)

a) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
b) \(=\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{2}+1\)
c) \(=\sqrt{\left(2\sqrt{2}+3\right)^2}=2\sqrt{2}+3\)
d) \(=\sqrt{\left(3-\sqrt{5}\right)^2}=3-\sqrt{5}\)
e) \(=\sqrt{\left(4-\sqrt{6}\right)^2}=4-\sqrt{6}\)
f) \(=\sqrt{\left(3+\sqrt{7}\right)^2}=3+\sqrt{7}\)
l) \(=\sqrt{\left(\sqrt{2}-\dfrac{1}{2}\right)^2}=\sqrt{2}-\dfrac{1}{2}\)
m) \(=\sqrt{\left(2\sqrt{2}+\dfrac{1}{4}\right)^2}=2\sqrt{2}+\dfrac{1}{4}\)

Với m = 3 thì (d): y = 8x - 7
PTHĐGĐ của (P) và (d): \(x^2-8x+7=0\)
Có: \(a+b+c=1+\left(-8\right)+7=0\)
=> PT có 2 nghiệm phân biệt \(x_1=1;x_2=7\)
\(x_1=1\Rightarrow y_1=x_1^2=1^2=1\\ x_2=7\Rightarrow y_2=x_2^2=7^2=49\)
Tọa độ giao điểm của (P) và (d) là: \(\left(1;1\right);\left(7;49\right)\)
b)
PTHĐGĐ của (P) và (d) là:
\(x^2-2\left(m+1\right)x+3m-2=0\)
\(\Delta'=\left(m+1\right)^2-\left(3m-2\right)=m^2+2m+1-3m+2=m^2-m+3\\ =m^2-m+\dfrac{1}{4}+\dfrac{11}{4}=\left(m-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall m\)
Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=3m-2\end{matrix}\right.\)
Theo đề: \(x_1^2+x_2^2=20\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4=20\\ \Leftrightarrow4m^2+2m+8-20=0\\ \Leftrightarrow4m^2+2m-12=0\\ \Leftrightarrow2m^2+m-6=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=-2\left(tm\right)\\m=\dfrac{3}{2}\left(tm\right)\end{matrix}\right.\)
Gọi tọa độ của \(\left(P\right),\left(d\right)\) là \(A\left(x_A;y_A\right),B\left(x_B;y_B\right)\)
\(a,m=3\)
\(\Rightarrow x^2=2\left(3+1\right)x-3.3+2\)
\(\Rightarrow x^2-8x+7=0\)
\(\Rightarrow\left\{{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Thay \(x=7\) vào \(\left(P\right):y=x^2\Rightarrow y=7^2=49\)
Khi m = 3 thì đường thẳng \(\left(d\right):y=2\left(3+1\right)x-3.3+2=8x-7\)
Thay \(x=1\) vào \(\left(d\right):y=8x-7=8.1-7=1\)
Vậy \(A\left(7;49\right),B\left(1;1\right)\)
\(\Rightarrow y=\left(2m+2\right)x-3m+2\)
\(b,\) Vì \(\left(P\right)\) và \(\left(d\right)\) luôn cắt nhau tại 2 điểm pb A,B \(\forall m\) nên :
\(x^2=2\left(m+1\right)x-3m+2\Leftrightarrow x^2-2\left(m+1\right)x+3m-2\)
Theo Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+2\\x_1x_2=\dfrac{c}{a}=3m-2\end{matrix}\right.\)
Ta có : \(x_1^2+x_2^2=20\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\)
\(\Leftrightarrow\left(2m+2\right)^2-2\left(3m-2\right)=20\)
\(\Leftrightarrow4m^2+8m+4-6m+4-20=0\)
\(\Leftrightarrow4m^2+2m-12=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m=-2\end{matrix}\right.\)
Vậy \(m=\dfrac{3}{2},m=-2\) thì thỏa mãn đề bài.

\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)

mai bạn tách ra nha để vậy hơi nhiều
c1: theo ct: \(I=\dfrac{U}{R}\)=>U tỉ lệ thuận I =>I càng lớn thì U càng lớn
C2(bn làm đúng)
C3: \(=>Umax=Imax.R=40.\dfrac{250}{1000}=10V\)=>chọn C
c4: R1 nt(R2//R3) =>U2=U3 mà R2=R3=>I2=I3
\(=>I1=I2+I3=>I2=I3=\dfrac{I1}{2}\)
C5: R1 nt R2
mà \(I1=2A,I2=1,5A\)=>chọn I2\(=>I1=I2=Im=1,5A=>Umax=\left(R1+R2\right).1,5=90V\)
C6: R1//R2
\(=>U1=I1R1=30V,U2=I2R2=15V\)=.chọn U2
C7\(=>\dfrac{1}{RTd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=>Rtd=6\left(om\right)\)
C8-\(=>I=\dfrac{U}{\dfrac{R1R2}{R1+R2}}=0,9A\)
\(=>I1=\dfrac{U}{R1}=\dfrac{12}{20}=0,6A=>I2=0,3A\)
C9-\(=>U3=\left(\dfrac{U1}{R1}\right)R3=8V=>Um=U1+U2+U3=....\)
(thay số vào)
C10\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=>Rtd=......\)(thay số)
C11: các bóng đèn như nhau nên mắc vào chung 1 nguồn điện nối tiếp sẽ hoạt động với đúng cường độ dòng điện định mức nên các bóng đều sáng bth=>chọn B
C12 \(\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}\)=>chọn D
c13\(=>R=\dfrac{U}{I}=\dfrac{6}{0,3}=20\left(om\right)\)
c14 R1 nt R2
\(R1=\dfrac{3}{0,3}=10\left(om\right),R2=\dfrac{6}{0,5}=12\left(om\right)=>I1=I2=\dfrac{11}{R1+R2}=0,5A=>I1>I\left(đm1\right),I2=I\left(đm2\right)\)
=>đèn 1 sáng mạnh hơn bth có thể hỏng , đèn 2 sáng bth
c15.\(=>\dfrac{R1}{R2}=\dfrac{S2}{S1}=>\dfrac{R1}{6}=\dfrac{1}{3}=>R1=2\left(om\right)\)
c16.\(=>l=\dfrac{RS}{p}=\dfrac{\left(\dfrac{U}{I}\right)S}{p}=\dfrac{\left(\dfrac{220}{5}\right).2.10^{-6}}{0,4.10^{-6}}=220m\)
c17.=>\(S'=3S,=>l'=\dfrac{1}{3}l\)
\(=>\dfrac{R}{R'}=\dfrac{\dfrac{pl}{S}}{\dfrac{pl'}{S'}}=\dfrac{S'.l}{S.l'}=\dfrac{3S.l}{S.\dfrac{1}{3}.l}=9=>R=9R'=>R'=\dfrac{R}{9}=1\left(om\right)\)
c18.chọn dây dẫn R3 có l3=l2,S3=S1,chùng chất liệu đồng
\(=>\dfrac{R1}{R3}=\dfrac{l1}{l3}=>\dfrac{1,7}{R3}=\dfrac{100}{200}=>R3=3,4\left(om\right)\)
\(=>\dfrac{R2}{R3}=\dfrac{S3}{S2}=>\dfrac{17}{3,4}=\dfrac{10^{-6}}{S2}=>S2=2.10^{-7}m^2\)\(=0,2mm^2\)
c19 \(l1=8l2,S1=2S2\)
\(=>\dfrac{R1}{R2}=\dfrac{\dfrac{pl1}{S1}}{\dfrac{.pl2}{S2}}=\dfrac{S2.l1}{S1.l2}=\dfrac{S2.8l2}{2S2.l2}=4=>R1=4R2\)
c20.\(=>R=\dfrac{0,9}{15}=0,06\left(om\right)\)(đáp án đề sai)
c21\(=>l=\dfrac{RS}{p}=\dfrac{10.10^{-7}}{0,4.10^{-6}}=2,5m\)
c22\(=>R=\dfrac{pl}{S}=\dfrac{6.1;7.10^{-8}}{3,14.\left(\dfrac{0,0012}{2}\right)^2}=0,09\left(om\right)\)

17 qủa trứng ứng với phân số là:
1 - \(\dfrac{1}{5}\) - \(\dfrac{3}{8}\) = \(\dfrac{17}{40}\) ( số trứng)
Số trứng người đó đem bán là:
17 : \(\dfrac{17}{40}\) = 40 (quả)
Lần thứ nhất người đó bán:
40 \(\times\) \(\dfrac{1}{5}\) = 8 (quả)
Lần thứ hai người đó bán:
40 \(\times\) \(\dfrac{3}{8}\) = 15 (quả)
Đs...
17 qủa trứng ứng với phân số là:
1 - 1551 - 3883 = 17404017 ( số trứng)
Số trứng người đó đem bán là:
17 : 17404017 = 40 (quả)
Lần thứ nhất người đó bán:
40 ×× 1551 = 8 (quả)
Lần thứ hai người đó bán:
40 ×× 3883 = 15 (quả)
đáp số
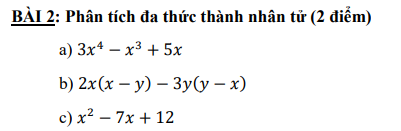
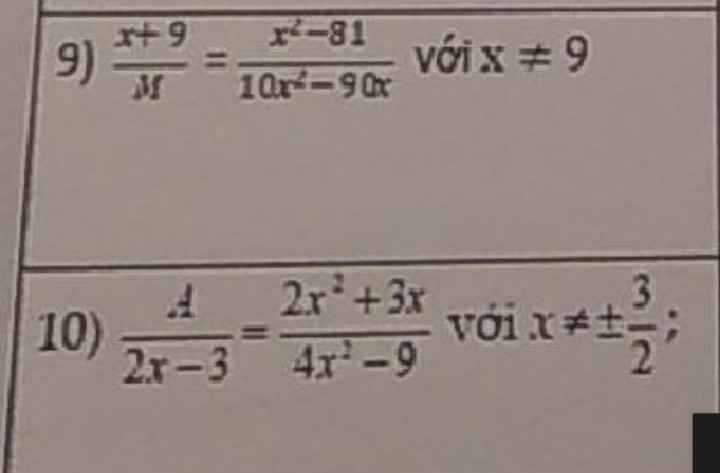

 Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn
Giúp mình bài này với ạ, mình cần lời giải chi tiết. Mình cảm ơn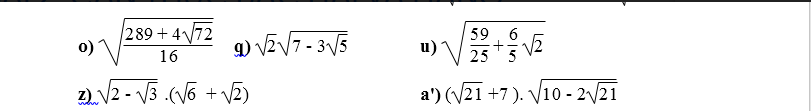








Câu 3:
a. \(\dfrac{5}{12}+\dfrac{7}{12}\)=\(\dfrac{12}{12}=1\)
b. \(\dfrac{9}{4}-\dfrac{-7}{5}=\dfrac{45}{20}-\dfrac{-28}{20}=\dfrac{73}{20}\)
c.\(\dfrac{-5}{7}+\dfrac{3}{4}+\dfrac{-1}{5}+\dfrac{-2}{5}+\dfrac{1}{4}\)
=\(\left(\dfrac{-5}{7}+\dfrac{-2}{7}\right)+\left(\dfrac{3}{4}+\dfrac{1}{4}\right)+\dfrac{-1}{5}\)
=\(\dfrac{-7}{7}+\dfrac{4}{4}+\dfrac{-1}{5}\)
= -1+ 1 +\(\dfrac{-1}{5}\)
= 0 + \(\dfrac{-1}{5}\)=\(\dfrac{-1}{5}\)
a) 5/12+ 7/12
= 12/12
=1
b) 9/4- (-7/5)
= 9/4+ 7/5
=45/ 20+ 28/ 20
= 73/ 20