trời ơi cứu tui cứu tui
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 1 2023
\(2^{2x+1}-4^x=16^x\)
\(\Leftrightarrow2^{2x}.2-4^x=\left(4^2\right)^x\)
\(\Leftrightarrow4^x.2-4^x=4^{2x}\)
\(\Leftrightarrow4^x=4^{2x}\)
\(\Leftrightarrow x=2x\)
\(\Leftrightarrow x=0\)
cứu tui mn ơi
NH
31 tháng 1 2023
sửa lại nhé
\(\left\{{}\begin{matrix}3\left(x-y\right)-y=11\\x-2\left(x+5y\right)=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\end{matrix}\right.\)
\(< =>\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)
Y
31 tháng 1 2023
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\left(1\right)\end{matrix}\right.\)
Nhân \(-3\) vào \(\left(1\right)\)
\(\left\{{}\begin{matrix}3x-4y=11\left(2\right)\\3x+30y=45\left(3\right)\end{matrix}\right.\)
Lấy \(\left(2\right)-\left(3\right)\) :
\(\Leftrightarrow3x-3x-4y-30y=11-45\)
\(\Leftrightarrow-34y=-34\)
\(\Leftrightarrow x=1\)
Lấy \(x=1\) thay vào \(\left(2\right)\) : \(3.1-4y=11\Leftrightarrow y=2\)
Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(1;2\right)\)
21 tháng 1 2023
Đề: Có ở trên
a) Khi nào nó là 1 phân số?
b) Khi nào nó là một số nguyên?
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 8 2023
Em tách nhỏ ra để hỏi, không đăng cả đề như thế này, em nhé!
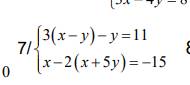
Ta có \(\dfrac{a^3}{a^2+b^2}=a-\dfrac{ab^2}{a^2+b^2}\ge a-\dfrac{ab^2}{2ab}=a-\dfrac{b}{2}=\dfrac{2a-b}{2}\)(áp dụng cosi cho \(a^2+b^2\ge2ab\))
\(\dfrac{b^3}{b^2+1}=b-\dfrac{b}{b^2+1}\ge b-\dfrac{b}{2b}=b-\dfrac{1}{2}=\dfrac{2b-1}{2}\)(áp dụng cosi cho\(b^2+1\ge2b\))
\(\dfrac{1}{a^2+1}=1-\dfrac{a^2}{a^2+1}\ge1-\dfrac{a^2}{2a}=1-\dfrac{a}{2}=\dfrac{2-a}{2}\)( áp dụng cosi cho \(a^2+1\ge2a\))
Cộng vế theo vế
\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+1}+\dfrac{1}{a^2+1}\ge\dfrac{2a-b+2b-1+2-a}{2}\)\(\ge\dfrac{a+b+1}{2}\left(đpcm\right)\)
Dấu "=" xảy ra <=> a=b=1